
Réglage
du One Tank par Iterative Feedback Tuning
Pierre Ansay - Emmanuel De Geest
Institut d'électricité Montefiore
- Service Systèmes
Grande
Traverse , 10 - 4000 Sart-Tilman
Belgique
Tel: +32 4 366 26 61
e-mail
: {ansay,degeest}@montefiore.ulg.ac.be
Introduction
Ce
laboratoire a pour but de procéder au réglage automatique des gains d’un
contrôleur PID sur un procédé de réglage de hauteur d’eau : le « One
Tank ». Nous rajouterons à ce système de laboratoire un délai artificiel
(logiciel) sur la grandeur de commande, afin de réguler un type de système
fréquemment rencontré dans l'industrie.
Le réglage automatique des gains sera réalisé
via l’utilisation d’un algorithme récent – l’Iterative Feedback Tuning – qui
impliquera de travailler en procédant à des expériences sur la boucle fermée
réelle. Cette méthode nous permettra
d’améliorer itérativement les gains d’un régulateur existant. Cet algorithme ne
nécessite aucune modélisation au préalable du système à réguler.
Le régulateur choisi est un PID, ce qui
nécessitera le réglage de trois
paramètres.
Nous utiliserons un algorithme MatlabÒ développé par le Service Systèmes pour implémenter l'Iterative Feedback
Tuning . Cette algorithme IFT sera commandé par une interface graphique GUI
(Graphical User Interface) en vue de simplifier au maximum son utilisation.
Tout a également été prévu pour que l'algorithme MatlabÒ IFT communique facilement avec
le programme LabviewÒ développé pour commander le One-Tank.
Le présent document est organisé comme suit:
Le premier paragraphe présente de manière
succincte le "One-Tank". Le second paragraphe établira la philosophie
du réglage par Iterative Feedback Tuning dans le cadre d'une régulation du
suivi de consigne. Le troisième paragraphe présentera le régulateur PID discret
utilisé. Les paragraphes 4 et 5 détaillent respectivement l’utilisation de
l’interface de commande LabviewÒ
et de l’interface GUI qui pilote
l’algorithme MatlabÒ IFT. Le paragraphe 6 donne le mode opératoire de l’expérience que nous
vous proposons de réaliser.
1.
Dispositif expérimental : le "One-Tank"
Le
Three-Tank (figure1) est un système hydraulique à trois réservoirs alimenté par
deux pompes actionnées indépendamment. Ce système peut avoir différentes
configurations.
Dans le
cadre de ce laboratoire, nous n’utiliserons que le réservoir R2 . Nous
travaillerons donc sur une configuration
de type "One Tank". Le but sera de réguler la hauteur d’eau du
réservoir R2. La vanne VF 3-2 sera constamment fermée. Le débit
d'eau entrant sera fourni par la pompe P2.Cette pompe sera à même de fournir un
débit variable dans la plage 0 à 100 ml/sec. La vanne de fuite (constamment
ouverte) sera la vanne VP 2 , la vanne de perturbation sera VF 2-0 . Nous n'aurons pas besoin
de donner pour ce laboratoire les caractéristiques du réservoir et des vannes
utilisées, vu que nous nous proposons justement de réguler le système
indépendamment de cette connaissance.
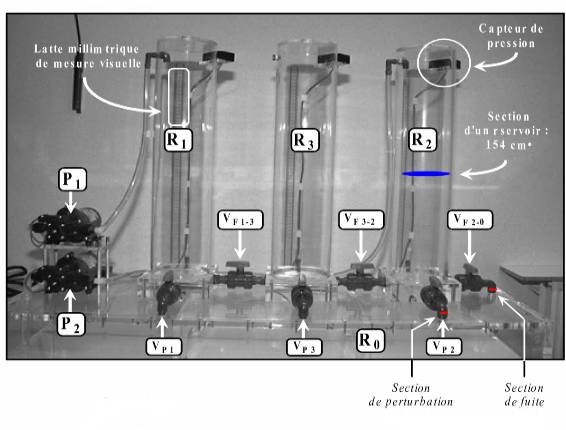
Figure 1 :Représentation du dispositif expérimental
Ce
système est un système non-linéaire dont la dynamique linéarisée autour d'un
point d'équilibre est du premier ordre. Or, dans la réalité industrielle,
beaucoup de systèmes s'identifient comme étant des systèmes du premier ordre
avec délai. Dès lors, en vue de cibler ce genre de système, nous avons rajouté
un délai artificiel - implémenté sur le programme LabviewÒ - sur la grandeur de commande. La valeur de ce
délai pourra être changé au gré de l'utilisateur.
2.
Iterative Feedback Tuning
Les méthodes de réglages classiques reposent
sur la connaissance d’un modèle du système.
Dans cette section, nous présentons une méthode
de réglage – l’Iterative Feedback Tuning - ne nécessitant aucune connaissance a
priori de la dynamique du système, mais impliquant simplement de devoir
travailler sur la boucle fermée réelle.
Cette méthode, récemment développée par H.
Hjalmarsson, S. Gunnarson et M. Gevers [1] , sera appliquée dans le cadre de la régulation du One-Tank par un
contrôleur PID.
Il s’agit d’une méthode optimale basée sur la
minimisation d’un critère de type quadratique dans lequel apparaît
explicitement l’erreur entre la sortie de la boucle fermée obtenue
expérimentalement et la réponse
désirée. Un second terme peut pénaliser l’effort de commande.
Il ne sera donc plus question d’une étape de
modélisation. L’idée présente dans cette méthode est de remplacer cette étape
par une modélisation directe des données recueillies en boucle fermée. Cela
débouchera sur un schéma itératif d’expériences menées en boucle fermée et de
mise à jour des paramètres du régulateur.
Cette section jette les bases théoriques de la
méthode. Le lecteur se référera à [1] pour de plus amples informations.
2.1
Critère de synthèse
Considérons le système de commande représenté à la figure 2. Nous ne disposons d’aucune information sur le procédé G(q). Les expressions mathématiques du système commandé au moyen d’un contrôleur à deux degrés de liberté C={Cr, Cy} sont (2.1):
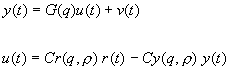
Dans ces expressions, r représente le vecteur des paramètres du contrôleur, q le délai, G(q) la fonction de transfert inconnue et temps-discret du système, t représente les instants temps-discret et u(t), r(t), y(t) et v(t) sont respectivement la séquence de commande, la séquence de consigne, la séquence de sortie et une séquence de bruit additif.
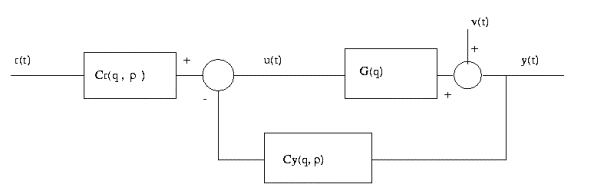
Figure 2 : Contrôleur à deux
degrés de liberté.
L'idée
de Hjalmarsson et al. est de synthétiser ce contrôleur C={Cr, Cy} de telle
manière que la sortie du système régulé soit la plus proche possible - au sens
quadratique - de la réponse d'un modèle de référence Td.
Cette
réponse est donnée par (2.2) :
![]()
Nous
allons alors calculer r* = arg min J(r) , où le critère à minimiser peut s'écrire
(2.3):
r
![]()
expression
dans laquelle
![]()
Le
premier terme pénalise donc la différence entre la sortie désirée yd et
la sortie réalisée y(r,t). Le second terme par
contre pénalise l'effort de commande.
2.2 Minimisation du critère
Nous
nous intéressons maintenant à la minimisation de J(r), c'est-à-dire à l'annulation de son
gradient par rapport au vecteur r des paramètres du
contrôleur. Afin de faciliter la notation, nous supposerons dans cette section
que Ly = Lu = 1.
Nous cherchons donc à résoudre l'équation (2.4):
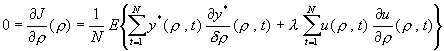
A
cause de la complexité de l'expression de y* en fonction de r et surtout de notre
méconnaissance du système G ainsi que du spectre des perturbations v qui
interviennent tous deux dans l'expression de y* , une méthode
itérative de minimisation s'impose. Nous allons donc effectuer une série
d'étapes i, de pas gi pour atteindre un minimum
local de la fonction de coût (2.5):
![]()
![]()
Ri devant être
une matrice définie positive. Il peut s'agir d'une matrice unité, mais la
convergence sera plus rapide si Ri est une estimation de la matrice
hessienne de J(r).
Ce
problème, tel que posé à ce stade ne sera soluble que si nous sommes en mesure
de calculer le gradient de la fonction de coût.
L'originalité
de l'IFT est de montrer qu'il est possible de remplacer le gradient réel de la
fonction de coût par une approximation non-biaisée, basée sur les échantillons
recueillis sur la boucle fermée.
Pour
ce faire, on a besoin de y*(ri) et de u(ri), ainsi que de leur
gradient.
2.3 Estimée des gradients
La théorie de l’Iterative Feedback Tuning donne des estimations non-biaisées pour les gradients de y*(ri) et de u(ri), calculées à partir de certaines expériences en boucle fermée.
Il est possible de dériver l’expression théorique de y*(r) par rapport à r, on obtient après artifice de calcul (2.6):
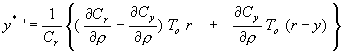
Nous procéderons alors à chaque pas d’itération i aux trois expériences suivantes (2.7) :
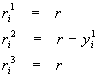
Les
sorties correspondantes sont
respectivement (2.8):
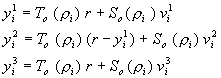
A
chaque pas d'itération, nous nous servirons des trois signaux de sortie obtenus
pour calculer y*(ri) et une estimée de son
gradient (2.9):
![]()
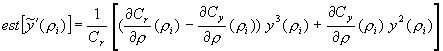
Notons
encore que cette section n'aborde que le calcul de l'estimée du signal y*. Des
considérations peuvent être tenues de manière similaires pour le signal u (voir
[1]).
En
remplaçant les grandeurs intervenant
dans le calcul du vrai gradient de la fonction de coût par leur estimée, on
obtient alors l'estimée du gradient de la fonction de coût. Cette formule ne
fait intervenir que des éléments calculables à partir des trois expériences
réalisées en boucle fermée. On démontre que cette estimée est une estimée
non-biaisée (2.10):
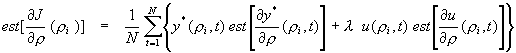
2.4
Résumé de l'algorithme
Nous
venons de jeter les bases de l'algorithme IFT. Le lecteur désirant rentrer dans
les détails théoriques complet de la méthode consultera la référence [1].
Les
aspects liés à l'implémentation de l'IFT, tels que le choix du nombre de
d'échantillons, le choix de la valeur du pas d'adaptation, l'introduction de
poids temporels dans la fonction de coût
et le choix du modèle de référence sont
discutés dans [2].
Jusqu'à
présent, la théorie de l'Iterative Feedback Tuning s'attachait exclusivement au
problème du suivi de consigne. Il est possible de reformuler un algorithme IFT
dans le cadre d'un problème de rejet de perturbations. Vient alors à l'esprit
de problème qui consiste à concilier ces deux problèmes, à savoir comment
trouver de bons gains qui optimisent
conjointement le problème du suivi de consigne et celui du rejet de
perturbations. Le lecteur consultera également [2] pour de plus amples
renseignements.
Enfin,
nous résumons brièvement l'algorithme
IFT sous sa forme théorique:
Soit
l'étape i de l'algorithme.
Le
vecteur des paramètres du régulateur à cette étape est ri .
(1)
On génère les signaux les
trois signaux de sorties yj , j=1,2,3 , et les trois signaux de
commande uj , j=1,2,3 ,
correspondant aux trois signaux d'entrée rj , j=1,2,3 donnés
à l'expression (2.7)
(2)
On calculera alors y*(ri) et est[y* '(ri)] via les relations (2.9).
On fera la même chose pour les grandeurs
équivalentes liées au signal u.
(3)
On calcule alors l'approximation stochastique du gradient donnée par
(2.10).
![]()
(4)Les nouveaux
paramètres du contrôleur sont calculés par:
(5) On passe à l'étape i+1.
3. Régulateur PID
La
figure 3 montre la structure de la boucle de régulation utilisée dans la cadre de
ce laboratoire. Nous restreignons donc à un schéma de contrôle à un degré de
liberté. Il suffira alors dans de poser dans l'algorithme IFT présenté
précédemment Cr =Cy. On démontre dans ce cas que seul les deux premières
expériences sont suffisantes afin d'obtenir une estimation non-biaisée du
gradient de la fonction de coût .
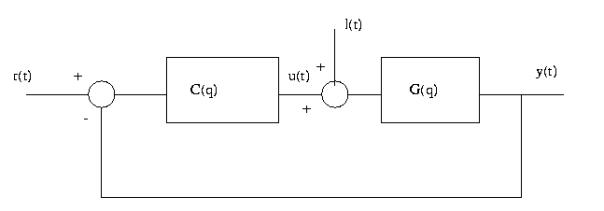
Figure 3 : Boucle de régulation utilisée au laboratoire
Le
contrôleur discret aura comme fonction de transfert (3.1):
![]()
Ce
régulateur est l'équivalent discret du régulateur PID continu mis sous sa forme
parallèle. Nous avons dès lors trois paramètres à trouver : K, Ki et Kd. Notons encore que h est la période
d'échantillonnage.
Un
système à retard est caractérisé par une phase décroissante en fonction du
logarithme de la fréquence. Avec cette
structure, on comprend aisément que l'on ne devra pas choisir des gains trop
importants afin de ne pas déstabiliser le système.
4.
Interface de commande LabviewÒ
Nous
donnons ici une description de l'utilisation de l'interface de commande du
One-Tank. Sur chacun des panneaux figure un nombre romain; Nous donnons d'abord une description de
chacun de ces panneaux (figure 4):
I
: On peut
régler la plage temporelle d'observation des graphes. Le bouton RAZ sert à
effacer les graphiques. Il convient de
l'actionner en début d'expérience.
II
: Ce
panneau nous donne le temps parcouru depuis le moment où on a lancé le
programme.
III
: On règle ici le point de fonctionnement du
système par l'intermédiaire du potentiomètre "Hauteur de consigne".
Le potentiomètre "Echelon de consigne" sert à simuler une expérience de suivi de consigne. Il importe
alors d'activer cela grâce au bouton
"Actif / Inactif".
Vous disposez aussi d'un indicateur permettant de voir la consigne appliquée tout au long des expériences.
IV
: Ce
panneau nous donne les gains courant pendant l'expérience. Ces gains sont ceux
donnés par l'IFT. Labview va lire les valeurs des gains dans un fichier
texte (init.txt) situé dans le
répertoire d:/Iterative Feedback Tuning /h2 . Notons encore que ce
fichier est lu une seule fois en début d'expérience et donc qu'il n'est pas
possible de changer les valeurs des gains en cours d'expérience.
V
: Vous avez ici l'indication de la hauteur
d'eau du réservoir R2. Celle-ci est mesurée une fois par période
d'échantillonnage.
VI
: Ce
panneau est le panneau de commande pour réaliser des expériences IFT. Nous
avons d'abord un bouton START
EXPERIENCE qui permet de choisir l'instant de début d'une expérience. Ceci est nécessaire car dans toutes les
expériences, il conviendra d'abord de stabiliser le système autour d'un de ses
points de fonctionnement avant de procéder à une expérience IFT
proprement-dit. Les indicateurs N et h
donnent respectivement le nombre de données à collecter ainsi que la période
d'échantillonnage. Encore une fois, ces valeurs sont lues dans le fichier
init.txt . EXPERIENCE ON est un
indicateur allumé lors d'une expérience IFT. Nous avons aussi une indicateur
nous permettant de juger quant à l'état d'avancement de l'expérience (NUMERO
ECHANTILLON). Au lancement de START
EXPERIENCE, on rajoute un incrément de consigne dont la valeur est lue dans le
fichier ref.txt (répertoire d:/Iterative
Feddback Tuning/h2). Ce fichier a
lui aussi été généré par notre algorithme IFT.
VI
et VIII : Graphiques
de l'évolution temporelle de la consigne, de la hauteur du réservoir R2 ainsi
que de la commande.
IX
: Réglage
du délai logiciel introduit sur la commande. Il peut être changé au cours d'une
expérience.
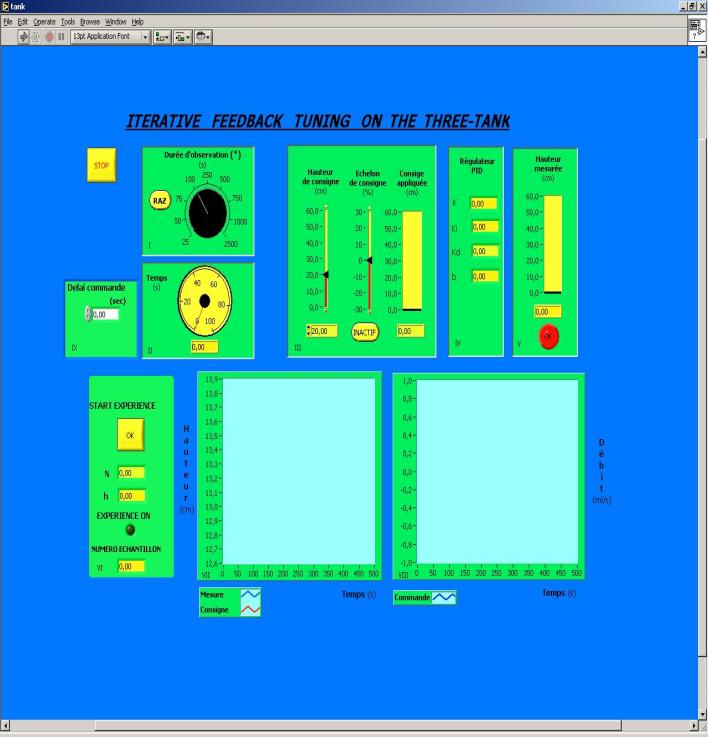
Remarquons encore que
le programme de commande s'arrêtera automatiquement à la fin d'une expérience
IFT. Le bouton STOP aura le même effet mais à n'importe quel moment.
Figure 4 :
Interface de commande LabviewÒ pour l'Iterative Feedback
Tuning
5.
Interface logicielle GUI pour l'IFT
Nous avons développé une interface GUI (Graphical
User Interface) de Matlab® qui permet d'appliquer les algorithmes IFT sur des
procédés réels. Celui-ci communiquera avec le logiciel de contrôle LabviewÒ à
l'aide d'un protocole de communication d'envoi et de réception de fichiers de
type TEXTE.
Le second objectif de ce logiciel a été de
définir une plate-forme commune pour une grande variété de régulateur discrets
classiques. Dans le cadre de ce laboratoire, nous nous sommes limités à la
structure du PID mixte explicitée à la section 3. Le logiciel a été toutefois
développé pour permettre n'importe quelle structure de régulateur.
La figure 5 montre la fenêtre principale du
programme. Dans cette figure, nous distinguons différents menus qui permettent
de parcourir les différentes étapes de l'algorithme IFT. On y trouve également
deux graphes qui vont présenter les données aux différentes étapes de
l'algorithme ainsi que la possibilité de définir les paramètres du régulateur
que nous voulons optimiser.
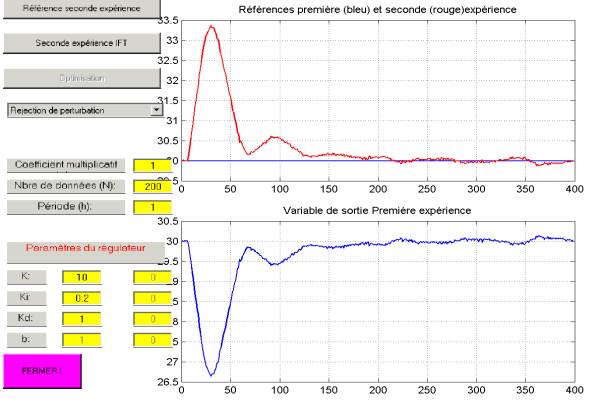
Figure
5 : Interface GUI pour l'Iterative Feedback Tuning
Les différents accès à partir de cette fenêtre
sont :
-
Initialisation: Cette
fonction est accessible via le bouton initialisation ; il permet le choix du
régulateur (PI mixte , PID mixte , compensateur de temps CTM et réglage d'un PI
avec structure CTM), le choix du mode de régulation (asservissement ou rejet de
perturbation de type charge), le nombre de données à collecter, la période
d'échantillonnage et le point de fonctionnement. Dans ce laboratoire nous
utilisons la forme mixte du PID.
-
Première et troisième expérience IFT: La seconde étape du logiciel est d'acquérir les données du procédé.
Dans cette version du logiciel, les premières et troisièmes expériences seront
réalisées en même temps.
-
Génération de la trajectoire: Cette troisième étape permet de générer la trajectoire pour la seconde expérience. Cette trajectoire est
fonction des données acquises lors de la première expérience et du mode de
régulation choisi.
-
Seconde expérience: La
seconde expérience consiste à injecter la trajectoire et à récolter les données
du procédé.
-
Optimisation: La
cinquième et dernière étape de la GUI est la phase d'optimisation des
paramètres du régulateur. En fonction du mode de régulation et du type de
régulateur, les paramètres du régulateurs sont ajournés. Le tuning de ces
paramètres est paramétrable comme suit:
·
Choix du pas d'optimisation γ : L'auteur intéressé consultera [2] pour de plus amples
renseignements.
·
Choix d'un éventuel filtre
temporel à appliquer : L'application d'un filtre
temporel sur la fonction de coût à minimiser permet d'améliorer les
performances de l'algorithme (voir [2]).
·
Choix de la constante de
temps du filtre appliqué à la référence: On
a choisi de générer la référence de sortie pour l'asservissement par un modèle
du premier ordre dont seul la constante de temps est à spécifier. C'est d'elle
dont il s'agit ici. Rappelons encore une fois que la référence que choisie lors
d'un réglage sur le rejet de perturbation est une référence constamment nulle
autour du point de fonctionnement.
Nous venons donc de résumer les étapes à
adopter en vue d'une utilisation correcte de l'algorithme. A présent, tous les
outils ont été construit pour procurer un maximum d'aisance à
l'automaticien.
6. Expérience Proposée
Régler le One-Tank qui présente un délai
artificiel de 10 secondes autour du point de fonctionnement correspondant à une
hauteur d'eau de 30 cm pour le réservoir R2. Les gains initiaux pourront être
choisis par une méthode simple (méthode temporelle ou fréquentielle). Ces gains
initiaux seront alors améliorés par l'intermédiaire de l'IFT et des outils
logiciels présentés précédemment. Ils sont disponibles dans le répertoire
d:/Iterative Feedback Tuning/h2 de la machine Three-Tank du laboratoire d'Automatique.
Bibliographie
[1]
Iterative Feedback Tuning : Theory and Applications, H. Hjalmarsson,
M.Gevers, S. Gunnarson and O. Lequin , IEEE Control Systems, pp26-41,
August 1998.
[2] Méthodes
d'optimisation pour le réglage de contrôleurs PID , Emmanuel De Geest , Travail
de fin d'études , Université de Liège , Faculté des
Sciences Appliquées, Liège, Belgique, Juin
2001.