Laboratoire 1¶
Les notions abordées dans ce laboratoire sont les suivantes:
Mathématique:
La règle de trois.
La dérivée et la dérivée seconde.
Physique:
Les unités et la conversion entre unités.
Le mouvement rectiligne uniforme à une dimension
La vitesse et l’accélération instantanées.
Le mouvement rectiligne uniformément accéléré à une dimension.
Programmation Python:
les tuples.
les fonctions.
les types entier et réel.
les variables globales et les effets de bord.
Programme 1: Conversion entre unités¶
Ce premier projet vise à vous familiariser avec le système de coordonnées utilisé au cours de ces laboratoires, et à vous exercer aux mécanismes de conversion entre différentes unités.
Systèmes de coordonnées¶
Nous allons travailler avec un programme qui gère une fenêtre. A l’intérieur de celle-ci, le système de coordonnées utilisé pour effectuer des opérations graphiques est le suivant:
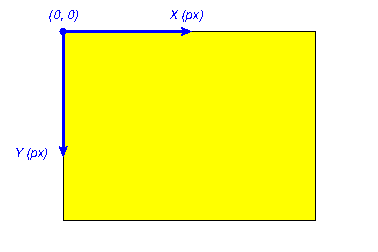
Système de coordonnées de la fenêtre.¶
Dans ce système, les coordonnées \((x, y)\) d’un point sont exprimées en pixels (abréviation: px). L’origine \((0, 0)\) du repère est située en haut à gauche. L’axe \(X\) va de gauche à droite, et l’axe \(Y\) de haut en bas. Les pixels sont carrés; en d’autres termes, leur largeur à l’écran est égale à leur hauteur.
Le programme doit être capable d’afficher un terrain de jeu dans la fenêtre. Afin de nous repérer sur ce terrain, nous allons définir un système de coordonnées plus commode à utiliser:
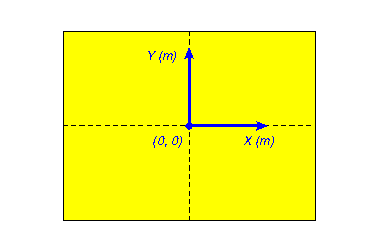
Système de coordonnées du terrain de jeu.¶
Dans ce système, les coordonnées \((x, y)\) d’un point sont exprimées en mètres (m). L’origine \((0, 0)\) du repère est située au centre du terrain. L’axe \(X\) va de gauche à droite, et l’axe \(Y\) de bas en haut.
Conversion depuis le terrain vers la fenêtre¶
Votre premier objectif consiste à écrire les deux fonctions suivantes:
une fonction
dist_terrain_vers_fenetre()capable de convertir une distance mesurée sur le terrain (en mètres) en une longueur dans la fenêtre (en pixels). Cette fonction doit:accepter trois arguments:
un réel
dist_treprésentant une distance sur le terrain.un entier
largeur_fenetredonnant la dimension horizontale de la fenêtre.un réel
largeur_terraindonnant la dimension horizontale du terrain.
retourner un réel
dist_fcontenant la conversion dedist_ten pixels.
une fonction
coord_terrain_vers_fenetre()capable de convertir les coordonnées d’un point depuis le système de coordonnées du terrain vers celui de la fenêtre. Cette fonction doit:accepter trois arguments:
un tuple
(x_t, y_t)contenant les coordonnées d’un point dans le repère du terrain.un tuple d’entiers
(largeur_fenetre, hauteur_fenetre)donnant les dimensions de la fenêtre (en pixels).un réel
largeur_terraindonnant la dimension horizontale du terrain.
retourner un tuple
(x_f, y_f)contenant la conversion de(x_t, y_t)dans le repère de la fenêtre.
Procédure à suivre:
Ecrire des formules exprimant:
dist_fen fonction dedist_t,largeur_fenetre,largeur_terrain.x_fety_fen fonction dex_t,y_t,largeur_fenetre,hauteur_fenetreetlargeur_terrain.Note: Vous pouvez y faire intervenir la fonction obtenue au point précédent.
Télécharger le programme prog-1.py.
Note: Si les caractères accentués ne s’affichent pas correctement dans votre navigateur, il est nécessaire de spécifier manuellement que la page est encodée en Unicode.
Dans ce programme, remplacer les fonctions
dist_terrain_vers_fenetre()etcoord_terrain_vers_fenetre()par votre propre implémentation des formules obtenues au point 1.Note: Dans un premier temps, ne modifier que ces deux fonctions. Le programme comprend d’autres fonctions modifiables qui seront traitées plus tard.
Vérifier que l’exécution du programme produit le résultat suivant:

Fenêtre du programme 1.¶
Reporter les formules obtenues au point 1 sur votre feuille de laboratoire (Code P1-1).
Conversion depuis la fenêtre vers le terrain¶
Vous avez peut-être remarqué que lorsque vous cliquez (avec le bouton gauche de la souris) sur un point de la fenêtre du programme 1, les coordonnées de ce point sont affichées dans le coin inférieur gauche.
Dans la version du programme que vous avez téléchargée, l’affichage des coordonnées est incorrect: les valeurs sont exprimées en pixels, mais affichées en mètres!
Pour corriger cela, il faut mettre à jour les deux fonctions suivantes:
la fonction
dist_fenetre_vers_terrain()est chargée de convertir une distance mesurée dans la fenêtre (en pixels) en une longueur sur le terrain (en mètres). Cette fonction:accepte trois arguments:
un réel
dist_freprésentant une distance dans la fenêtre.un entier
largeur_fenetredonnant la dimension horizontale de la fenêtre.un réel
largeur_terraindonnant la dimension horizontale du terrain.
retourne un réel
dist_tcontenant la conversion dedist_fen mètres.
une fonction
coord_fenetre_vers_terrain()capable de convertir les coordonnées d’un point depuis le système de coordonnées de la fenêtre vers celui du terrain. Cette fonction:accepte trois arguments:
un tuple
(x_f, y_f)contenant les coordonnées d’un point dans le repère de la fenêtre.un tuple d’entiers
(largeur_fenetre, hauteur_fenetre)donnant les dimensions de la fenêtre (en pixels).un réel
largeur_terraindonnant la dimension horizontale du terrain.
retourne un tuple
(x_t, y_t)contenant la conversion de(x_f, y_f)dans le repère du terrain.
Procédure à suivre:
Ecrire des formules exprimant:
dist_ten fonction dedist_f,largeur_fenetre,largeur_terrain.x_tety_ten fonction dex_f,y_f,largeur_fenetre,hauteur_fenetreetlargeur_terrain.Note: Comme précédement, vous pouvez y faire intervenir la fonction obtenue au point 1a.
Dans votre version courante du programme
prog-1.py, remplacer les fonctionsdist_fenetre_vers_terrain()etcoord_fenetre_vers_terrain()par votre propre implémentation des formules obtenues au point 1.Vérifier que les coordonnées affichées par le programme lorsque l’on clique dans la fenêtre sont correctes.
Reporter les formules obtenues au point 1 sur votre feuille de laboratoire (Code P1-2).
Conversion de temps¶
La dernière étape de ce projet consiste à convertir des unités temporelles. Le programme 1 est capable de mesurer le délai qui sépare deux clics consécutifs de la souris. Par défaut, ce délai est exprimé en tics, un tic correspondant à la période de rafraîchissement de la fenêtre.
Par exemple, dans la version actuelle de notre programme, la fenêtre est rafraîchie 50 fois par seconde, ce qui entraîne qu’un tic correspond à 20 millisecondes.
La conversion en secondes d’une durée exprimées en tics est
réalisée par une fonction temps_tics_vers_secondes(), que vous
allez implémenter. Cette fonction doit:
accepter deux arguments:
un entier
t_treprésentant une durée exprimée en tics.un entier
tics_par_secondedonnant le nombre de rafraîchissements de la fenêtre par seconde.
retourner un réel
t_scorrespondant à la duréet_tconvertie en secondes.
Procédure à suivre:
Ecrire une formule exprimant
t_sen fonction det_tettics_par_seconde.Dans votre version courante du programme
prog-1.py, remplacer la fonctiontemps_tics_vers_secondes()par votre implémentation de la formule obtenue au point précédent.Vérifier que la durée séparant deux clics rapides de la souris est correctement affichée par le programme (dans le coin inférieur droit de la fenêtre).
Reporter la formule obtenue au point 1 sur votre feuille de laboratoire (Code P1-3).
Programme 2: Jeu de tir¶
Notre deuxième projet porte sur le développement d’un jeu de tir. Dans un premier temps, celui-ci doit afficher une fenêtre semblable à celle-ci:
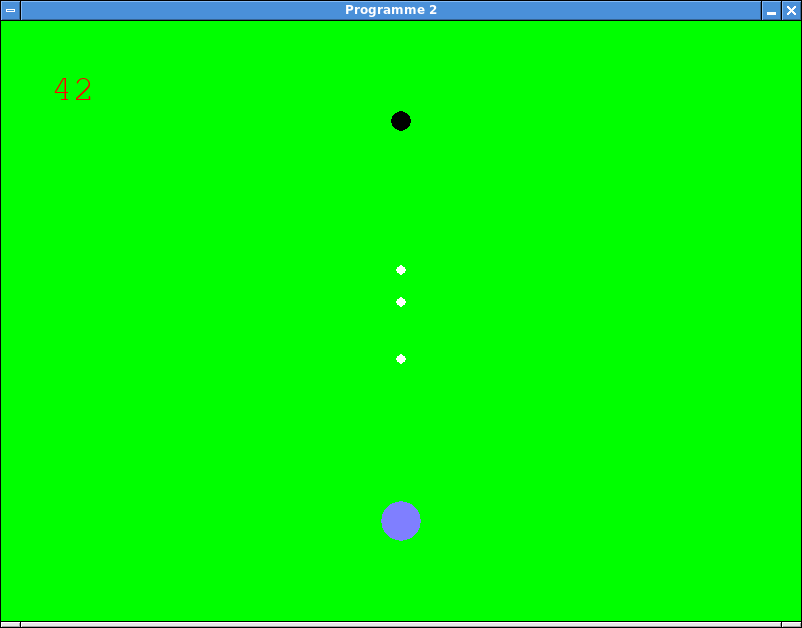
Fenêtre du programme 2.¶
Le disque bleu situé au bas de la fenêtre représente la zone de tir. Chaque fois que l’on clique avec la souris, un projectile est émis à partir de cette zone, en direction de la cible représentée par le disque noir. Les projectiles n’ont pas tous la même vitesse: Un clic gauche produit un projectile lent, et un clic droit un projectile rapide.
La cible n’est pas fixe, mais oscille sur une ligne horizontale. Lorsqu’elle est touchée par un projectile, le score (affiché en rouge) est incrémenté.
Mouvement des projectiles¶
Les projectiles se déplacent selon un mouvement rectiligne uniforme à une seule dimension, dans la direction de l’axe vertical de la fenêtre. Dans le programme, chaque projectile est représenté par une structure de données qui contient:
sa position sur l’axe vertical au moment où il a été lancé.
sa vitesse selon l’axe vertical.
l’instant auquel il a été lancé.
Votre travail consiste tout d’abord à implémenter une fonction
mru_1d() capable de calculer la position courante d’un projectile à
un instant donné. Cette fonction doit:
accepter quatre arguments:
un entier
departreprésentant la position de départ d’un mobile dans un espace à une dimension, exprimée en pixels.un entier
temps_departreprésentant l’instant de départ, exprimé en millisecondes.un réel
vitessereprésentant la vitesse du mobile, exprimée en pixels/milliseconde.un entier
temps_maintenantdonnant l’instant présent, exprimé en millisecondes. Cet instant peut être supposé supérieur ou égal àtemps_depart.
retourner un réel
pcorrespondant à la position du mobile à l’instant présent.
Procédure à suivre:
Ecrire une formule exprimant
pen fonction dedepart,temps_depart,vitesseettemps_maintenant.Télécharger le programme prog-2.py.
Dans ce programme, remplacer la fonction
mru_1d()par votre propre implémentation de la formule obtenue au point 1.Note: Dans un premier temps, ne modifier que cette fonction.
Vérifier que le programme fonctionne correctement.
Reporter la formule obtenue au point 1 sur votre feuille de laboratoire (Code P2-1).
Tir automatique¶
Etant donné que le mouvement des projectiles est entièrement prévisible, l’étape suivante consiste à calculer précisément le moment où il faut tirer afin d’atteindre la cible lorsqu’elle est située juste à la verticale du canon.
Pour ce faire, vous devez définir une fonction calculer_tir()
possédant les caractéristiques suivantes. Cette fonction doit:
accepter cinq arguments:
un entier
departreprésentant la position de départ d’un projectile, dans un espace à une dimension, exprimée en pixels.un entier
ciblereprésentant la position de la cible, dans le même système de coordonnées.un réel
vitessereprésentant la vitesse du projectile que l’on est capable de tirer, exprimée en pixels/milliseconde.un entier
prochain_temps_cibleindique le prochain instant où la cible sera à la verticale du canon. Ce temps est exprimé en millisecondes.un entier
temps_maintenantdonnant l’instant présent, exprimé en millisecondes. Ce temps peut être supposé inférieur ou égal àprochain_temps_cible.
retourner une paire de valeurs:
un booléen
tir_est_possibleindiquant s’il est possible ou non d’effectuer un tir atteignant la cible à l’instant indiqué.dans le cas où
tir_est_possibleest vrai, l’instanttemps_tiroù il faut tirer afin d’atteindre la cible.Note: Dans le cas où
tir_est_possibleest faux, la valeur detemps_tirretournée peut être quelconque.
Procédure à suivre:
Ecrire la condition déterminant la valeur de
tir_est_possibleen fonction des paramètres du problème.Ecrire une formule exprimant, lorsque
tir_est_possibleest vrai, la valeur detemps_tiren fonction des paramètres du problème.Dans votre version courante du programme
prog-2.py, remplacer la fonctioncalculer_tir()par votre propre implémentation des formules obtenues aux points 1 et 2.Vérifier le bon fonctionnement du programme. Le tir automatique peut être activé en pressant la touche “L” pour un projectile lent, ou “R” pour un projectile rapide.
Note: Lorsqu’un tir automatique est programmé, la zone de tir change de couleur. Si le tir automatique n’est pas possible (parce que la cible ne peut pas être atteinte lors de son prochain passage), ce changement de couleur n’a pas lieu.
Reporter les formules obtenues aux points 1 et 2 sur votre feuille de laboratoire (Code P2-2).
Programme 3: Avion¶
Le troisième projet de ce laboratoire vise à étudier les mouvements d’un avion. Celui-ci possède une vitesse horizontale constante, et ses mouvements verticaux sont contrôlés par la souris: A chaque instant, l’altitude de l’avion correspond à la position verticale du pointeur de la souris. La situation est illustrée ci-dessous.
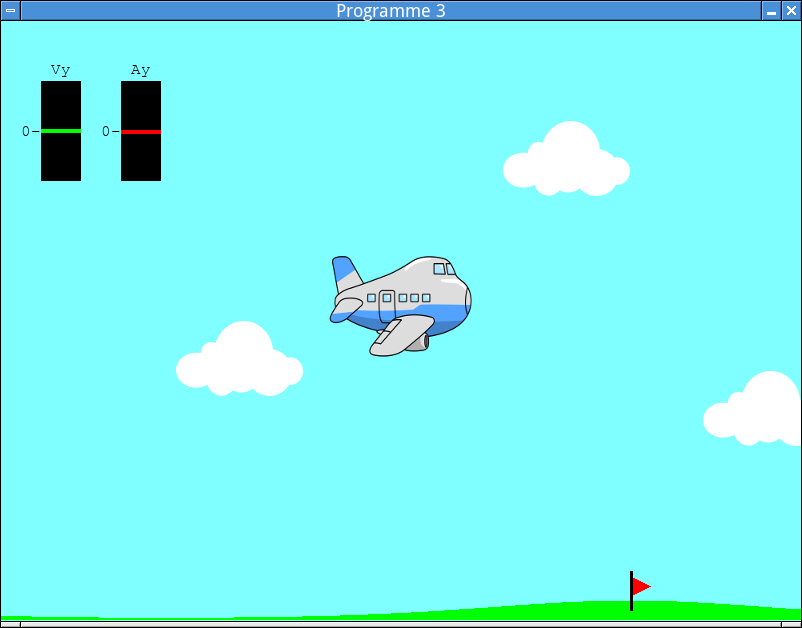
Fenêtre du programme 3.¶
Instruments de bord¶
Les instruments de bord visibles dans le coin supérieur droit de la fenêtre correspondent à
un variomètre, qui affiche la vitesse instantanée \(V_y\) de l’avion selon l’axe vertical. Cette valeur est positive lorsque l’avion monte et négative lorsqu’il descend.
un accéléromètre, qui affiche l’accélération instantanée \(A_y\) de l’avion selon l’axe vertical. Cette valeur est positive lorsque la vitesse verticale instantanée \(V_y\) augmente, et négative lorsqu’elle diminue.
Note: L’accélération \(A_y\) correspond à la vraie accélération qui peut-être calculée en observant les mouvements de l’avion, et non à celle qui pourrait être mesurée par un dispositif physique embarqué à bord. En effet, cette dernière, appelée accélération propre, inclut nécessairement l’effet de la gravité. Par exemple, pour un avion volant à une altitude constante, on a \(A_y = 0\), alors qu’un accéléromètre embarqué indiquera une acceleration verticale de 1 g dirigée de bas en haut. Vos téléphones portables permettent probablement d’installer des applications affichant leur accélération propre instantanée. N’hésitez pas à expérimenter afin de vous familiariser avec ces notions!
Dans la version de base du programme 3, ces instruments sont inactifs
et affichent constamment une valeur nulle. Votre premier objectif consiste
à les faire fonctionner en calculant à chaque instant la valeur de
\(V_y\) et \(A_y\), dans une fonction appelée
calculer_vitesse_acceleration(). Cette fonction doit:
accepter deux arguments:
un entier
altitude_aviondonnant la position verticale de l’avion à l’instant présent. Cette position correspond au nombre de pixels qui séparent le haut de la fenêtre et le centre de l’avion. Attention, avec cette convention, lorsque l’avion monte, sa position verticale diminue!un entier
temps_maintenantdonnant l’instant auquel la position de l’avion a été mesurée, exprimé en millisecondes.
retourner un tuple de réels
(Vy, Ay)correspondant à la vitesse et à l’accélération verticale de l’avion, exprimées en:pixels/milliseconde pour
Vy,pixels/(milliseconde au carré) pour
Ay.
Pour implémenter cette fonction, nous avons besoin d’un mécanisme de programmation particulier. Il n’est en effet pas possible de déterminer la valeur de \(V_y\) et \(A_y\) sur la seule base de l’altitude de l’avion à l’instant courant: Les valeurs précédentes de ces variables doivent intervenir dans le calcul.
Pour mémoriser ces valeurs précédentes, la solution la plus simple consiste à utiliser des variables globales, dont la valeur reste préservée entre des appels successifs de la fonction. Par exemple, vous pouvez modifier la valeur d’une telle variable lors d’un appel de la fonction, et la consulter lors de l’appel suivant. (On dit alors que la fonction possède un effet de bord.)
Note: En Python, il est nécessaire d’utiliser le mot-clé global
pour indiquer quelles sont les variables globales manipulées par une
fonction.
Enfin, il est nécessaire de pouvoir attribuer une valeur initiale
aux variables globales qui seront manipulées par la fonction
calculer_vitesse_acceleration(). Ces initialisations peuvent
s’effectuer dans une fonction initialiser_calculs() qui sera
invoquée (une seule fois) avant le premier appel à
calculer_vitesse_acceleration().
Procédure à suivre:
Ecrire des formules exprimant \(V_y\) et \(A_y\) sur base des valeurs courantes et passées de
altitude_avionettemps_maintenant.Télécharger le programme prog-3.zip.
En plus du programme Python proprement dit, cette archive contient un répertoire d’images (pour l’avion et les nuages). Décomprimer cette archive (
unzip prog-3.zip) et verifier que le programme fonctionne correctement: la position verticale de l’avion doit suivre les mouvements de la souris.Dans ce programme, remplacer les fonctions
initialiser_calculs()etcalculer_vitesse_acceleration()par votre propre implémentation des formules obtenues au point 1.Note: La version de base de ces fonctions montre comment définir et manipuler une variable globale. N’hésitez pas à renommer cette variable, et à en utiliser d’autres!
Vérifier que l’affichage du variomètre et de l’accéléromètre fonctionne correctement.
Reporter les formules obtenues au point 1 sur votre feuille de laboratoire (Code P3-1).
Lâcher de bombes¶
Bien que le type d’avion dessiné ne corresponde pas exactement à un bombardier, nous allons maintenant ajouter à notre programme un mécanisme permettant de larguer des bombes.
Lorsqu’une bombe est lâchée par l’avion, elle garde la même vitesse horizontale que celui-ci, et tombe par le seul effet de la gravité. Cela implique que son mouvement vertical est uniformément accéléré. Par souci de simplicité, nous supposerons que la vitesse verticale initiale des bombes est nulle.
Dans le programme, chaque bombe est représentée par une structure de données qui contient:
sa position sur l’axe vertical au moment où elle a été larguée.
l’instant auquel elle a été larguée.
Votre travail consiste maintenant à implémenter une fonction
mrua_1d() capable de calculer la position verticale d’une bombe à
un instant donné. Cette fonction doit:
accepter quatre arguments:
un entier
departreprésentant la position de départ d’une bombe dans un espace à une dimension, exprimée en pixels.un entier
temps_departreprésentant l’instant de départ, exprimé en millisecondes.un réel
accelerationreprésentant l’acceleration subie par la bombe, exprimée en pixels/(milliseconde au carré).un entier
temps_maintenantdonnant l’instant présent, exprimé en millisecondes. Cet instant peut être supposé supérieur ou égal àtemps_depart.
retourner un réel
pcorrespondant à la position de la bombe à l’instant présent.
Procédure à suivre:
Ecrire une formule exprimant
pen fonction dedepart,temps_depart,accelerationettemps_maintenant.Dans votre version courante du programme
prog-3.py, remplacer la fonctionmrua_1d()par votre propre implémentation de la formule obtenue aux points 1 et 2.Vérifier le bon fonctionnement du programme. Des bombes peuvent être larguées en pressant la touche “B”.
Reporter la formule obtenue aux point 1 sur votre feuille de laboratoire (Code P3-2).
Largage automatique¶
Tout comme pour le deuxième programme, le mouvement de l’avion et la trajectoire des bombes est entièrement prévisible. Il est donc possible de calculer précisément l’instant où il faut larguer une bombe de façon à atteindre une cible (représentée par un drapeau).
Pour ce faire, vous devez définir une fonction calculer_tir()
possédant les caractéristiques suivantes. Cette fonction doit:
accepter cinq arguments:
un entier
altitude_largagereprésentant la position de largage d’une bombe, dans un espace à une dimension (l’axe vertical), exprimée en pixels.un entier
altitude_ciblereprésentant la position de la cible, dans le même système de coordonnées.un réel
accelerationreprésentant l’accélération subie par une bombe au cours de sa chute, exprimée en pixels/(milliseconde au carré).un entier
prochain_temps_cibleindique le prochain instant où la cible sera à la verticale de l’avion. Ce temps est exprimé en millisecondes.un entier
temps_maintenantdonnant l’instant présent, exprimé en millisecondes. Ce temps peut être supposé inférieur ou égal àprochain_temps_cible.
retourner une paire de valeurs:
un booléen
tir_est_possibleindiquant s’il est possible ou non de larguer une bombe qui atteindra la cible à l’instant indiqué.dans le cas où
tir_est_possibleest vrai, l’instanttemps_tiroù il faut larguer la bombe afin d’atteindre la cible.Note: Dans le cas où
tir_est_possibleest faux, la valeur detemps_tirretournée peut être quelconque.
Procédure à suivre:
Ecrire la condition déterminant la valeur de
tir_est_possibleen fonction des paramètres du problème.Ecrire une formule exprimant, lorsque
tir_est_possibleest vrai, la valeur detemps_tiren fonction des paramètres du problème.Dans votre version courante du programme
prog-3.py, remplacer la fonctioncalculer_tir()par votre propre implémentation des formules obtenues aux points 1 et 2.Vérifier le bon fonctionnement du programme. Le tir automatique peut être activé en pressant la touche “A”.
Notes:
Lorsqu’un largage automatique est programmé, un message s’affiche en dessous des instruments de bord. Il ne s’affiche pas s’il est impossible d’atteindre la cible lors de son prochain passage.
Si l’avion modifie son altitude entre l’instant où un programme un largage et celui où l’on effectue celui-ci, la bombe manquera sa cible!
Reporter les formules obtenues aux points 1 et 2 sur votre feuille de laboratoire (Code P3-3).