Laboratoire 2

Les nouvelles notions abordées dans ce laboratoire sont les suivantes:

  • Mathématique:

    • Les fonctions trigonométriques élémentaires.

    • Les vecteurs.

    • La dérivée et la dérivée seconde d’un vecteur.

  • Physique:

    • Le vecteur vitesse et le vecteur accélération.

  • Programmation Python:

    • La bibliothèque mathématique.

Programme 4: Affichage de vecteurs

Dans ce laboratoire, nous allons manipuler des vecteurs à deux dimensions. Notre premier objectif consiste à construire un outil permettant de visualiser de tels vecteurs.

Plus précisément, le problème consiste, étant donné un vecteur \(\vec{v}\) et un point \(p\) du plan, à dessiner une flèche correspondant à \(\vec{v}\), et possédant \(p\) comme origine.

Pygame fournit une primitive permettant de dessiner des polygones. Nous allons l’utiliser pour dessiner, pour \(\vec{v}\) et \(p\) donnés, la forme suivante:

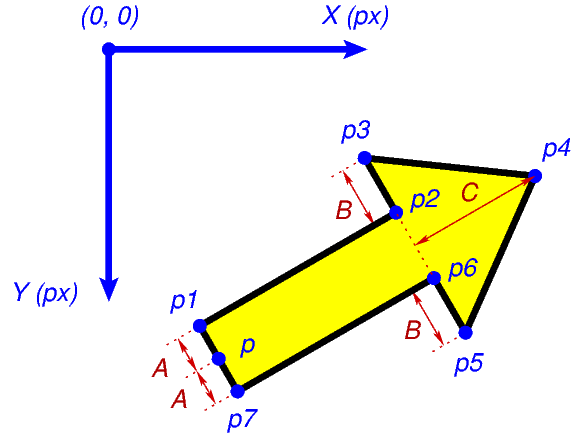
Forme d'un vecteur.

Forme d’un vecteur.

L’origine \(p\) est donc située au milieu de la base de la flèche. Le vecteur \(\vec{v}\) doit correspondre au déplacement qui amène \(p\) sur l’extrémité \(p_4\) de la flèche. En d’autres termes, on doit avoir

\(\vec{v}=\vec{pp_4}\).

La position des autres sommets \(p_1\), \(p_2\), \(p_3\), \(p_5\), \(p_6\) et \(p_7\) peut alors être déterminée sur base de \(\vec{v}\) et de \(p\), ainsi que des trois constantes \(A\), \(B\) et \(C\) représentées sur la figure. Remarquez que la figure présente des angles droits aux sommets \(p_1\), \(p_2\), \(p_6\) et \(p_7\).

Déplacement d’un point

Avant d’entamer le calcul de ces sommets, il est utile de construire un outil destiné à vous faciliter la vie. Votre première étape sera de définir une fonction deplacer_pol(point, distance, orientation) dont le but est de calculer les nouvelles coordonnées de point après l’avoir déplacé de la distance distance dans la direction donnée par orientation. Ce dernier paramètre correspond à l’angle formé par la direction du déplacement avec l’horizontale. Comme le système d’axes que nous utilisons possède un axe \(Y\) dirigé vers le bas, une valeur positive de orientation correspond à un déplacement vers le bas (à condition qu’elle reste inférieure à \(\pi\) radians!), et une valeur négative à un déplacement vers le haut. La situation est illustrée ci-dessous (cette figure montre donc un angle positif):

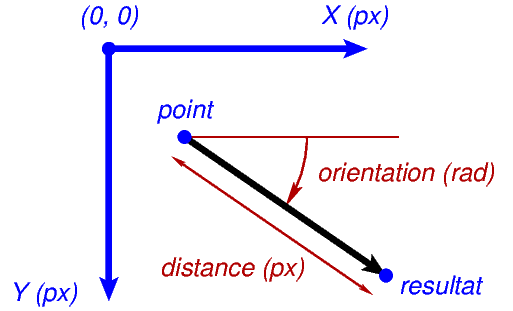
Déplacement d'un point dans une direction.

Déplacement d’un point dans une direction.

Si ce système de coordonnées un peu étrange vous pose problème, il suffit d’imaginer qu’il correspond à l’image de celui que vous avez l’habitude d’utiliser par un miroir horizontal. Le cercle trigonométrique, dans lequel les angles positifs représentent des rotations dans le sens contraire des aiguilles d’une montre, est donc lui-aussi inversé par ce miroir.

Coordonnées des sommets

Maintenant que vous disposez de cet outil, voici la marche à suivre pour calculer les sommets du polygone à partir de \(\vec{v}\) et \(p\):

  1. Calculer le point \(p_4\) égal à la translation de \(p\) par le vecteur \(\vec{v}\).

  2. Calculer l’angle \(\alpha\) que forme le vecteur \(\vec{v}\) avec l’horizontale, en utilisant les mêmes conventions que pour l’orientation sur la figure précédente.

    Note: Cette opération peut facilement s’implémenter grâce à la fonction atan2() de la bibliothèque math de Python: Etant donnés les deux côtés \(a\) (horizontal) et \(b\) (vertical) d’un triangle rectangle, l’expression math.atan2(b, a) retourne l’angle correspondant à l’orientation de son hypoténuse, comme l’illustre la figure suivante: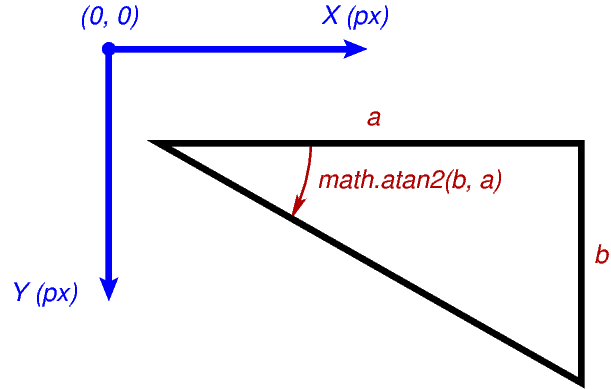

    math.atan2().

    math.atan2()

    Dans cet exemple, l’angle retourné est positif: Rappelez-vous que nous utilisons un systèmes de coordonnées où l’axe \(Y\) est inversé!

    Note: La fonction atan2() gère correctement les cas où \(a\) et \(b\) sont signés, ainsi que les situations où l’un de ces paramètres est nul.

  3. Calculer la position du point \(p_1\). Comme on le voit sur la figure, celui-ci peut s’obtenir en appliquant la fonction deplacer_pol() au point \(p\), avec une distance de déplacement égale à \(A\) et une orientation égale à \(\alpha - \frac{\pi}{2}\).

  4. D’une façon similaire, calculer la position de \(p_7\).

  5. Les coordonnées de \(p_2\) peuvent maintenant être calculées, en déplaçant \(p_1\) grâce à deplacer_pol(). Ce déplacement doit suivre l’orientation \(\alpha\). La distance de déplacement est égale à \(|pp_4| - C\), où \(|pp_4|\) désigne la distance séparant \(p\) et \(p_4\).

    Ce calcul met en évidence un problème potentiel: Si \(|pp_4|\) est plus petit que \(C\), alors la distance de déplacement sera négative, et la figure dessinée ne ressemblera pas à une flèche.

    Nous règlerons ce problème un peu plus tard, en considérant séparément le cas particulier où \(|pp_4| < C\). Pour le moment, nous supposerons \(|pp_4| \geq C\).

  6. Les coordonnées de \(p_6\) peuvent s’obtenir par la même démarche.

  7. La position de \(p_3\) peut s’obtenir en déplaçant \(p_2\) d’une distance égale à \(B\), selon l’orientation \(\alpha - \frac{\pi}{2}\).

  8. La position de \(p_5\) s’obtient de façon similaire.

A la fin de cette procédure, vous avez maintenant obtenu des formules pour l’ensemble des sommets \(p_1\), \(p_2\), \(p_3\), \(p_4\), \(p_5\), \(p_6\) et \(p_7\) du polygone correspondant à flèche. Reportez-les sur votre feuille de laboratoire (Code P4-1).

Notes:

  • Si nécessaire, vous pouvez utiliser plusieurs cases de la feuille!

  • Vous pouvez utiliser une abréviation pour la fonction deplacer_pol().

Cas d’un petit vecteur

Pour rappel, les calculs que vous venez d’effectuer ne sont valides que si la condition \(|pp_4| \geq C\) est satisfaite. Dans le cas contraire, le vecteur est trop petit pour pouvoir être affiché par une flèche complète.

Dans ce cas particulier, le motif que nous allons afficher est le suivant (on ne dessine que la tête de la flèche):

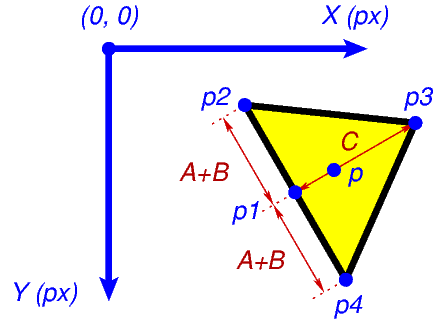
Forme d'un petit vecteur.

Forme d’un petit vecteur.

La procédure à suivre pour calculer les sommets est similaire au cas précédent:

  1. Calculer le point \(p_3\) égal à la translation de \(p\) par \(\vec{v}\).

  2. Calculer l’angle \(\alpha\) que forme le vecteur \(\vec{v}\) avec l’horizontale,

  3. Calculer les coordonnées de \(p_1\) en déplaçant \(p_3\) d’une distance égale à \(C\) selon l’orientation \(\alpha + \pi\). (Il s’agit de l’orientation exactement opposée à \(\alpha\).)

  4. La position de \(p_2\) correspond au déplacement de \(p_1\) selon la distance \(A+B\) et l’orientation \(\alpha - \frac{\pi}{2}\).

  5. La position de \(p_4\) s’obtient par une démarche similaire.

Dans ce cas particulier, les sommets du polygone à dessiner sont donc \(p_2\), \(p_3\) et \(p_4\). Reportez les formules donnant leur coordonnées sur votre feuille de laboratoire (Code P4-2).

Dessin d’une flèche

Tous les mécanismes sont maintenant en place pour pouvoir dessiner des vecteurs.

Procédure à suivre:

  1. Télécharger le programme prog-4.py.

  2. Dans ce programme, modifier les fonctions deplacer_pol() et dessiner_vecteur() en y incorporant le résultat de vos calculs.

    La fonction dessiner_vecteur() doit effectuer les opérations suivantes:

    1. Calculer la longueur du vecteur fourni en argument, et déterminer si cette longueur est inférieure ou non à \(C\).

    2. Dans les deux cas, calculer les coordonnées des sommets du polygone à dessiner.

    3. Construire une liste polygone contenant ces coordonnées. (contenant par exemple [ p1, p2, p3, p4, p5, p6, p7 ], où p1, p2, …, p7 correspondent aux sommets successifs).

    4. Exécuter pygame.draw.polygon(fenetre, couleur, polygone).

  3. Vérifier que le programme fonctionne correctement. Lorsque l’on clique sur deux points de la fenêtre, le vecteur reliant ces deux points doit être affiché. Un clic droit permet d’effacer la fenêtre.

    A titre d’exemple, voici un écran typique affiché par ce programme après un certain nombre de clics:

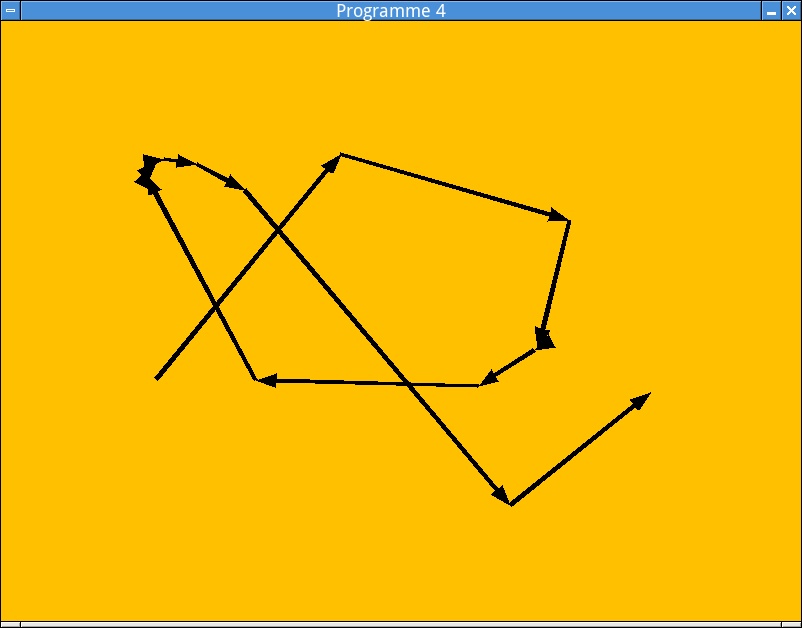
    Affichage du programme 4.

    Affichage du programme 4.

Programme 5: Vitesse et accélération en deux dimensions, détection de gestes

Maintenant que nous disposons d’un mécanisme capable d’afficher des vecteurs dans notre fenêtre, nous allons l’utiliser pour étudier les mouvement d’un mobile contrôlé par la souris.

Vecteurs vitesse et accélération

L’objectif est ici de visualiser en temps réel les vecteurs représentant la vitesse et l’accélération du mobile.

Procédure à suivre:

  1. Télécharger le programme prog-5.py.

  2. Dans ce programme, recopier vos fonctions deplacer_pol() et dessiner_vecteur() obtenues au point précédent.

  3. Modifier les fonctions initialiser_calculs() et calculer_vitesse_acceleration_2d() en suivant les mêmes principes que ceux du programme 3 (l’avion). La différence est que le calcul de la vitesse et de l’accélération doit maintenant s’effectuer dans un espace à deux dimensions.

    La fonction calculer_vitesse_acceleration_2d():

    • accepte deux arguments:

      • position, qui fournit la position courante du mobile, sous la forme d’un tuple à deux dimensions dont chaque composante est exprimée en pixels.

      • temps_maintenant, qui donne l’instant courant, exprimé en millisecondes.

    • retourne une paire (v, a), où

      • v est un tuple à deux dimensions donnant le vecteur vitesse instantané du mobile. Chaque composante de ce vecteur est exprimée en pixels par milliseconde.

      • a est un tuple à deux dimensions donnant le vecteur accélération instantanée du mobile. Chaque composante de ce vecteur est exprimée en pixels par milliseconde au carré.

  4. Si vos calculs sont corrects, vous devriez voir s’afficher les vecteurs vitesse (en rouge) et accélération (en vert) instantanés de votre mobile, au gré des mouvements de la souris.

    Note: En raison des unités utilisées (pixels par milliseconde et pixels par millisecondes au carré), les composantes des vecteurs calculés sont très petites. Avant d’afficher ces vecteurs, le programme les multiplie donc par des constantes appropriées afin qu’ils deviennent visibles.

    Prenez le temps d’expérimenter! Que se passe-t-il lorsque vous inversez brutalement la direction dans laquelle se déplace le mobile? Lorsque vous imprimez un mouvement circulaire à celui-ci? Lorsque vous suivez une trajectoire qui tourne dans un sens puis dans l’autre?

    Remarque: Vous pouvez activer ou désactiver l’affichage du vecteur vitesse en pressant la touche “V”, et celui du vecteur accélération en pressant la touche “A”.

  5. Reportez les formules que vous avez utilisées pour calculer les vecteurs vitesse et accélération sur votre feuille de laboratoire (Code P5-1).

Détection de gestes

Vos téléphones portables peuvent être contrôlés par des gestes que vous effectuez sur leur écran tactile. Certaines tablettes ou agendas électroniques sont capables de reconnaître l’écriture manuelle en interprétant les mouvements d’un stylet.

Nous allons à présent implémenter une version simplifiée d’un tel mécanisme, en exploitant le fait que les vecteurs vitesse et accélération sont disponibles. Le geste que nous cherchons à détecter correspond à réaliser un mouvement de bas en haut (le long de l’axe vertical), immédiatement suivi par un mouvement inverse, de haut en bas. L’objectif est, chaque fois que cela se produit, d’incrémenter la valeur du compteur affiché en haut à gauche dans la fenêtre.

Procédure à suivre:

  1. Dans le programme précédent (avec vos modifications), programmer la fonction detecter_geste() selon les principes suivants:

    • Comme le geste à détecter inclut une inversion du mouvement, il comprendra un point où le vecteur vitesse s’annule. En pratique, vu que l’utilisateur ne réalisera pas toujours un geste parfait, il faudra appliquer une certaine tolérance: Un geste ne peut être détecté que si, à un moment donné, le vecteur vitesse possède une longueur inférieure à 0.2 pixel par milliseconde.

    • Au moment où le mouvement s’inverse, lorsque la condition ci-dessus est vraie, le vecteur accélération doit indiquer une brusque modification du mouvement vers le bas. On va donc imposer deux conditions supplémentaires: La longueur du vecteur accélération doit dépasser 0.002 pixel par milliseconde au carré, et son orientation doit être verticale (avec une tolérance de plus ou moins 10 degrés), dirigée de haut en bas.

    • La fonction doit retourner True lorsque toutes les conditions sont satisfaites (ce qui signifie qu’un geste a été détecté) et False sinon.

  2. Vérifier que le programme fonctionne. Chaque geste correctement effectué doit provoquer une incrémentation du compteur.

  3. Reportez la formule que vous avez utilisée pour vérifier si le vecteur accélération possède une direction proche de la verticale sur votre feuille de laboratoire (Code P5-2).