Laboratoire 6¶
Les nouvelles notions abordées dans ce laboratoire sont les suivantes:
Physique:
L’énergie cinétique.
L’énergie potentielle gravitationnelle.
La conservation de l’énergie et de la quantité de mouvement.
Les collisions élastiques.
Programme 9: L’énergie d’un satellite¶
Pour ce programme, nous allons partir du programme 7 que vous avez
réalisé dans le cadre du laboratoire 4 (celui qui
simulait les mouvements d’un vaisseau spatial), et lui apporter
quelques modifications. La première étape consiste donc à recopier
prog-7.py dans un nouveau fichier prog-9.py.
Affichage de l’énergie cinétique¶
Pour commencer, nous allons ajouter un tableau de bord au programme, afin d’afficher à chaque instant l’énergie cinétique du vaisseau spatial.
Procédure à suivre:
Dans la fonction chargée de mettre à jour la position du vaisseau, calculer l’énergie cinétique de celui-ci (à partir de sa vitesse courante), et en placer la valeur dans une variable globale
energie_cinetique. Il ne faut bien sûr pas oublier de déclarer cette variable à l’aide du mot-cléglobaldans cette fonction.Pour rappel, dans le programme 7, nous avions utilisé des unités exotiques pour exprimer les forces: des tonnes fois pixels par milliseconde au carré plutôt que des Newtons. Par conséquent, l’énergie que nous calculons ici sera également exprimée dans une unité non standard plutôt qu’en Joules: en tonnes par pixels au carré par milliseconde au carré. (Rappel: 1 Joule = 1 kilogramme fois mètre carré par seconde au carré.)
En utilisant les mêmes mécanismes que dans le programme 8 du laboratoire 5, définir une fonction
afficher_tableau_de_bord()chargée d’afficher à l’écran la valeur instantanée de l’énergie cinétique du vaisseau. Afin d’obtenir une valeur facile à lire, vous pouvez pour cet affichage multiplier la valeur calculée par un facteur constant, par exemple 1000. (Cela revient à modifier l’unité dans laquelle l’énergie cinétique est exprimée.)Appeler cette fonction dans la boucle principale de votre programme, après avoir dessiné le vaisseau et la planète. L’objectif est d’arriver à un affichage similaire à celui-ci.
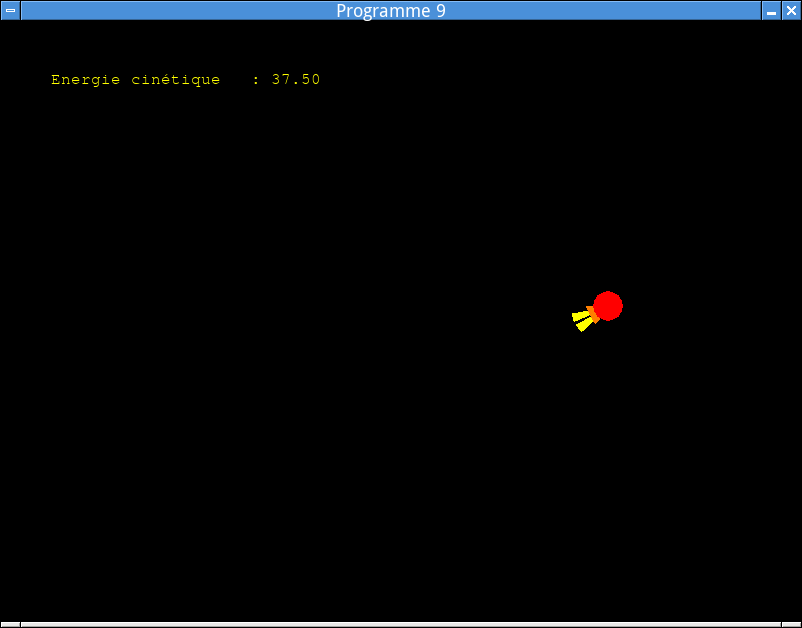
Affichage de l’énergie cinétique.¶
Affichage de l’énergie potentielle¶
L’étape suivante consiste, lorsque la planète est présente, à calculer et à afficher l’énergie potentielle du vaisseau par rapport à l’attraction gravitationnelle qu’elle exerce sur ce dernier. La valeur de cette énergie est donnée par la formule
\(\displaystyle U = -G\frac{m_1 m_2}{r}\),
où \(G\) est la constante gravitationnelle, \(m_1\) et \(m_2\) sont les masses respectives du vaisseau et de la planète, et \(r\) est la distance qui les sépare. Comme on le voit dans cette formule, l’énergie potentielle du vaisseau est toujours négative, et tend vers zéro lorsque celui-ci s’éloigne à l’infini de la planète.
Note: Pour que vos calculs soient cohérents, les unités utilisées pour représenter \(G\), \(m_1\), \(m_2\) et \(r\) doivent correspondre à celles employées dans le reste du programme: pixels au cube par tonne fois milliseconde au carré pour \(G\), tonnes pour \(m_1\) et \(m_2\), et pixels pour \(r\).
Procédure à suivre:
Dans la fonction chargée de mettre à jour la position du vaisseau, si la planète est présente, calculer l’énergie potentielle du vaisseau par rapport à l’attraction gravitationnelle de cette planète. Placer cette valeur dans une variable globale
energie_potentielle.Dans la fonction
afficher_tableau_de_bord(), si la planète est présente, afficher l’énergie potentielle du vaisseau, ainsi que la somme de ses énergies potentielle et cinétique. Note: Si vous avez utilisé un facteur multiplicatif pour changer l’unité d’affichage de l’énergie cinétique, il faut effectuer ici la même modification pour l’énergie potentielle.L’affichage devrait à présent ressembler à celui-ci. (Dans cet exemple, le rayon de la planète a été ramené à 20 pixels par rapport au programme 7.)
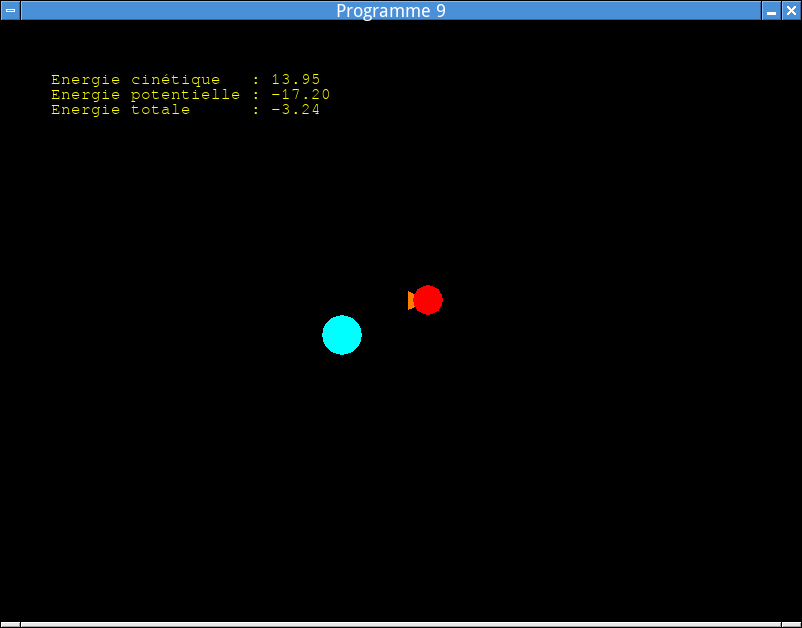
Affichage de l’énergie potentielle.¶
Conservation de l’énergie¶
Lorsque vous n’actionnez pas le propulseur, l’énergie totale du vaisseau devrait rester constante, sauf quand le vaisseau franchit la frontière de la fenêtre et se retrouve du côté opposé. Cela devrait être le cas, en particulier, lorsque le vaisseau est placé en orbite autour de la planète. Cette propriété est-elle vérifiée dans votre simulation?
Si la réponse est non, et que vos calculs sont corrects, alors le problème provient d’une imprécision numérique causée par une discrétisation trop grossière du temps. Pour effectuer une simulation plus précise, vous pouvez employer le même mécanisme que dans le programme 8 (les montagnes russes): Plutôt que de mettre à jour la position du vaisseau à chaque rafraîchissement de la fenêtre, les itérations vont être effectuées beaucoup plus fréquemment.
Marche à suivre:
Si vous avez suivi les consignes du laboratoire 4 lors du développement de votre programme initial, celui-ci devrait contenir une fonction
mettre_a_jour_position()chargée de calculer la position du vaisseau à chaque itération. Cette fonction admet, entre autres, un argumenttemps_maintenantdonnant l’instant courant exprimé en millisecondes.Comme vous l’avez fait pour les montagnes russes, l’objectif est à présent de modifier la boucle principale du programme de façon à appeler cette fonction un plus grand nombre de fois. La procédure est identique à celle du laboratoire 5. A chaque itération de la boucle principale, avant d’afficher le vaisseau et la planète, il faut:
Invoquer
pygame.time.get_ticks()afin de connaître l’instant courant.Définir une variable
temps_maintenantdestinée à accueillir cette valeur, et une autre variabletemps_precedentretenant la valeur detemps_maintenantlors de l’itération précédente.Effectuer une boucle faisant varier la valeur d’une variable
tdepuistemps_precedentjusqu’àtemps_maintenant - 1, par incréments d’une milliseconde. A chaque itération de cette boucle, invoquer la fonctionmettre_a_jour_position()en lui passant l’instant courantt.
Tester votre programme. L’énergie totale reste-t-elle maintenant constante lorsque le vaisseau n’actionne pas sa propulsion?
Si ce n’est toujours pas le cas, alors il faut augmenter davantage le nombre d’itérations effectuées entre deux rafraîchissements de la fenêtre. Une façon simple de le faire consiste à définir une constante
FACTEUR_SIMULATIONreprésentant le nombre d’itérations à effectuer par milliseconde de temps simulé. (Pour un premier essai, on peut attribuer par exemple la valeur 5 à cette constante.) Ensuite, on effectue les adaptations suivantes:Modifier la boucle sur
ten faisant varier cette variable detemps_precedent * FACTEUR_SIMULATIONà(temps_maintenant * FACTEUR_SIMULATION) - 1.Dans l’appel à
mettre_a_jour_position(), passer l’instant courantt / FACTEUR_SIMULATIONplutôt quet.Expérimenter de façon à trouver une valeur appropriée de
FACTEUR_SIMULATION. Comme vous le remarquez, une valeur élevée conduit à une simulation plus précise, mais au prix d’un temps de calcul supérieur. LorsqueFACTEUR_SIMULATIONdevient trop grand, le temps de calcul nécessaire ne permet plus une simulation en temps réel.
Lorsque votre programme fonctionne correctement, le déposer dans le répertoire centralisé, sous le suffixe
prog-9.py.
En expérimentant avec le simulateur, vous avez sans doute remarqué que l’énergie totale du vaisseau peut être positive ou négative. Avez-vous compris à quoi correspondent ces deux situations? (Souvenez-vous que l’énergie potentielle tend vers zéro lorsque le vaisseau s’éloigne à l’infini de la planète.)
Enfin, il est utile de rappeler que la propriété de conservation de l’énergie totale du vaisseau n’est satisfaite que parce que nous avons supposé que la planète est immobile. Si nous permettons à celle-ci de subir l’attraction gravitationnelle du vaisseau (en application de la troisième loi de Newton), alors le vaisseau peut parfois transférer une partie de son énergie vers la planète, et vice-versa. L’énergie totale du système composé du vaisseau et de la planète reste cependant bien sûr toujours constante.
Programme 10: Le billard spatial¶
Dans ce nouveau programme, nous allons modifier le comportement de la planète, de façon à permettre des collisions élastiques entre celle-ci et le vaisseau.
Procédure:
Recopier la dernière version de votre programme dans un nouveau fichier
prog-10.py.Modifier ce programme de façon à ce que:
La planète soit toujours présente.
Elle n’exerce plus d’attraction gravitationnelle sur le vaisseau.
Sa masse soit du même ordre de grandeur que celle du vaisseau (par exemple, 5 tonnes).
Sa position soit mise à jour à chaque appel de
mettre_a_jour_position(), de la même façon que celle du vaisseau.Initialement, puisqu’aucune force ne s’exerce encore sur la planète et que celle-ci possède une vitesse nulle, cette mise à jour laisse inchangée la position de la planète. Afin de tester votre code, vous pouvez cependant attribuer à la planète une vitesse initiale non nulle et vérifier qu’elle se déplace correctement. (N’oubliez pas de ramener cette vitesse initiale à zéro une fois le test effectué.)
Lorsque la planète sort de la fenêtre, elle réapparaît du côté opposé de la même façon que le vaisseau.
Note: Une bonne idée est d’utiliser la même fonction pour effectuer cette opération pour le vaisseau et pour la planète.
Tester soigneusement que les modifications apportées sont correctes.
Détection et calcul des collisions¶
L’étape suivante consiste à simuler des collisions élastiques entre le vaisseau et la planète, de façon à obtenir une sorte de billard spatial. Les principes sont les suivants:
Une collision est détectée lorsque la distance séparant le centre du vaisseau et le centre de la planète devient inférieure ou égale à \(r_1 + r_2\), où \(r_1\) est le rayon du vaisseau et \(r_2\) celui de la planète.
Appelons \(\vec{v_1}\) et \(\vec{v_2}\) les vecteurs vitesse respectifs du vaisseau et de la planète avant la collision, et \(m_1\) et \(m_2\) leurs masses.
Pour calculer les vecteurs vitesse \(\vec{v'_1}\) et \(\vec{v'_2}\) des deux mobiles après la collision, on procède de la façon suivante:
Si \(\vec{p}_1\) est la position du vaisseau et \(\vec{p}_2\) celle de la planète, en supposant que ces positions ne sont pas confondues, on pose
\(\vec{d} = \vec{p_2} - \vec{p_1}\)
et
\(\displaystyle \vec{u} = \frac{\vec{d}}{|\vec{d}|}\).
En d’autres termes, \(\vec{u}\) est un vecteur directeur unitaire de la droite reliant le centre du vaisseau au centre de la planète.
On décompose \(\vec{v_1}\) en \(\vec{v_1} = \vec{v_{1L}} + \vec{v_{1T}}\), où:
\(\vec{v_{1L}}\) est la composante de \(\vec{v_1}\) parallèle à \(\vec{u}\), c’est-à-dire
\(\vec{v_{1L}} = (\vec{v_1}.\vec{u}) \vec{u}\),
\(\vec{v_{1T}}\) est la composante de \(\vec{v_1}\) orthogonale à \(\vec{u}\), c’est-à-dire
\(\vec{v_{1T}} = \vec{v_1} - \vec{v_{1L}}\).
De la même façon, on décompose \(\vec{v_2}\) en \(\vec{v_2} = \vec{v_{2L}} + \vec{v_{2T}}\), où \(\vec{v_{2L}}\) et \(\vec{v_{2T}}\) sont respectivement parallèle et orthogonal à \(\vec{u}\).
Après la collision, les composantes \(\vec{v_{1T}}\) et \(\vec{v_{2T}}\) de la vitesse des deux mobiles restent inchangées, car les forces résultant de la collision ne s’exercent que dans la direction parallèle à \(\vec{u}\).
Sur l’axe \(\vec{u}\), le problème se réduit à une collision à une dimension, entre un mobile de vitesse \(v_1 = \vec{v_1}.\vec{u}\) et un autre de vitesse \(v_2 = \vec{v_2}.\vec{u}\) (ces vitesses étant mesurées avant la collision).
Pour calculer les vitesses \(v'_1\) et \(v'_2\) des mobiles sur l’axe \(\vec{u}\) après la collision, on utilise deux lois:
La conservation de la quantité de mouvement du système:
\(m_1 v_1 + m_2 v_2 = m_1 v'_1 + m_2 v'_2~~~~\) (1),
La conservation de l’énergie cinétique du système:
\(\displaystyle \frac{1}{2}m_1 (v_1)^2 + \frac{1}{2}m_2 (v_2)^2 = \frac{1}{2}m_1 (v'_1)^2 + \frac{1}{2}m_2 (v'_2)^2~~~~\) (2).
Le but est de résoudre ce système d’équations de façon à déterminer \(v'_1\) et \(v'_2\) en fonction des autres variables. Il ne s’agit pas d’une opération évidente. Voici une procédure permettant de l’effectuer:
Dans (1) et (2), déplacer vers le membre de gauche les termes dépendant de \(m_1\), et vers le membre de droite ceux dépendant de \(m_2\).
Dans la nouvelle expression de (2), factoriser chaque membre en exploitant les produits remarquables.
Diviser (2) par (1), en faisant attention au cas particulier où les deux membres de (1) sont identiquement nuls.
Utiliser le résultat pour exprimer \(v'_2\) en fonction de \(v_1\), \(v_2\) et \(v'_1\).
Injecter l’expression obtenue dans (1) pour obtenir l’expression de \(v'_1\) en tant que fonction de \(v_1\) et \(v_2\).
Obtenir une expression similaire pour \(v'_2\) par la symétrie du problème.
Une fois que \(v'_1\) et \(v'_2\) sont connus, on a finalement
\(\vec{v_1} = v'_1 \vec{u} +\vec{v_{1T}}\)
et
\(\vec{v_2} = v'_2 \vec{u} +\vec{v_{2T}}\)
qui donnent les vecteurs vitesse des deux mobiles après la collision.
Implémentation¶
Vous disposez maintenant de tous les outils nécessaires pour implémenter les collisions entre le vaisseau et la planète.
Marche à suivre:
Sur une feuille de papier, développez les calculs décrits au point précédent, en particulier les expressions de \(v'_1\) et de \(v'_2\).
Dans la fonction
mettre_a_jour_positions(), après avoir calculé la nouvelle vitesse du vaisseau, appeler une nouvelle fonctiongerer_collision_2d()chargée de gérer les collisions. Cette fonction doit recevoir en arguments les positions du vaisseau et de la planète, leurs masses, et leurs vecteurs vitesse avant la collision. Elle doit retourner les nouveaux vecteurs vitesse du vaisseau et de la planète.Programmer cette fonction
gerer_collision_2d()en implémentant le résultat des calculs obtenus au point 1. Il ne faut bien sûr pas oublier de détecter si une collision doit avoir lieu ou non.Si vous le souhaitez, vous pouvez modifier le tableau de bord en affichant l’énergie cinétique du vaisseau, celle de la planète, et leur somme.
Tester que votre programme fonctionne correctement.
Reporter les formules obtenues au point 1 pour \(v'_1\) et \(v'_2\) sur votre feuille de laboratoire (Code P10-1).
Déposer votre programme dans le répertoire centralisé, sous le suffixe
prog-10.py.
Si vous avez atteint ce stade avec un programme fonctionnel, félicitations, les lois du mouvement n’ont plus de secrets pour vous!
Vous êtes maintenant arrivé au terme de ces laboratoires. Nous espérons que ceux-ci vous ont permis d’acquérir une meilleure compréhension des concepts mathématiques et physiques abordés, et de renforcer votre expérience en programmation.
S’il vous reste du temps, vous pouvez (facultativement!) effectuer de qnouvelles découvertes en vous dirigeant vers la version avancée de ces laboratoires, principalement axée sur la mise en pratique de notions mathématiques dans le cadre d’applications amusantes.