Laboratoire 1

L’objectif de ce laboratoire est de vous familiariser avec la manipulation des nombres complexes.

L’environnement de programmation Python contient déjà une librairie permettant d’effectuer des opérations sur les nombres complexes, mais nous n’allons pas l’utiliser! Le but est ici d’implémenter par vous-même ces opérations.

Bibliothèque de manipulation de nombres complexes

En Python, on peut facilement représenter des nombres complexes par des tuples à deux composantes (c’est-à-dire, des couples): Le nombre \((a + bi)\) sera représenté par le tuple (a, b).

Votre premier objectif consiste à programmer les fonctions suivantes:

• Une fonction c_new(a, b) qui retourne le nombre complexe possédant la partie réelle \(a\) et la partie imaginaire \(b\).

• Une fonction c_re(z) qui retourne la partie réelle du nombre \(z\).

• Une fonction c_im(z) qui retourne la partie imaginaire du nombre \(z\).

• Une fonction c_add(x, y) qui calcule la somme \(x + y\) des deux nombres complexes \(x\) et \(y\).

• Une fonction c_mult(x, y) qui calcule le produit \(xy\) des deux nombres complexes \(x\) et \(y\).

• Une fonction c_div(x, y) qui calcule le quotient \(\frac{x}{y}\) des deux nombres complexes \(x\) et \(y\).

  Note: En cas de division par zéro, cette fonction peut retourner (math.nan, math.nan), correspondant à une valeur indéterminée.

• Une fonction c_conj(z) qui retourne le conjugué du nombre \(z\).

• Une fonction c_abs(z) qui retourne le module du nombre \(z\).

• Une fonction c_arg(z) qui retourne l’argument du nombre \(z\), exprimé en radians et compris entre \(-\pi\) et \(\pi\).

  Note: Une façon simple d’implémenter cette opération est d’exploiter la fonction math.atan2() de la bibliothèque standard Python.

• Une fonction c_new_pol(m, a) qui retourne le nombre complexe possédant le module \(m\) et l’argument \(a\) (exprimé en radians).

A titre d’exemple, voici un fragment de programme qui implémente les trois premières fonctions de cette liste:

import math

def c_new(a, b):
    return (a, b)

def c_re(z):
    a, b = z
    return a

def c_im(z):
    a, b = z
    return b

A vous de compléter ce programme avec les autres fonctions demandées.

Remarques:

• Les trois fonctions ci-dessus sont très simples, et peuvent facilement être contournées. Par exemple, on pourrait remplacer x = c_im(z), par l’instruction équivalente x = z[1]. L’intérêt d’utiliser de telles fonctions est qu’elles rendent les programmes modulaires: Si l’on décide un jour de représenter les nombres complexes à l’aide d’une autre structure de données, il sera possible d’effectuer cette modification sans que cela n’affecte les programmes qui utilisent ces fonctions, à condition que leur interface et leur effet ne soit pas altérés.
• Une bonne référence sur les nombres complexes se trouve sur le site de MathWorld.

Premier programme

Dans ce premier programme, vous allez mettre en place les mécanismes permettant de visualiser le plan complexe dans une fenêtre.

Procédure à suivre:

1. En vous inspirant du programme d’exemple fourni à la fin du guide rapide de Python et Pygame, rédigez un programme qui crée une fenêtre et la peint dans la couleur de fond de votre choix.

2. Incorporez à ce programme les fonctions de manipulation de nombres complexes que vous avez créées à la rubrique précédente. Ajoutez une nouvelle fonction afficher_complexe(z, c) qui affiche le nombre complexe z dans la fenêtre, avec la couleur c. Principes:

   • La dimension horizontale de la fenêtre s’étend sur 800 pixels et représente l’axe réel, de gauche à droite.

   • La dimension verticale s’étend sur 600 pixels et représente l’axe imaginaire, de bas en haut. (Attention: Dans Pygame, la coordonnée verticale des pixels croît du haut vers le bas, c’est-à-dire dans le sens opposé à celui qui nous intéresse.)

   • Le coin inférieur gauche de la fenêtre doit correspondre au nombre \(-2.5 - 1.5i\), et le coin supérieur droit au nombre \(1.5 + 1.5i\).

     Note: Une bonne idée consiste à spécifier ces valeurs en tant que paramètres, tout comme la taille en pixels de la fenêtre, afin de pouvoir facilement les modifier plus tard.

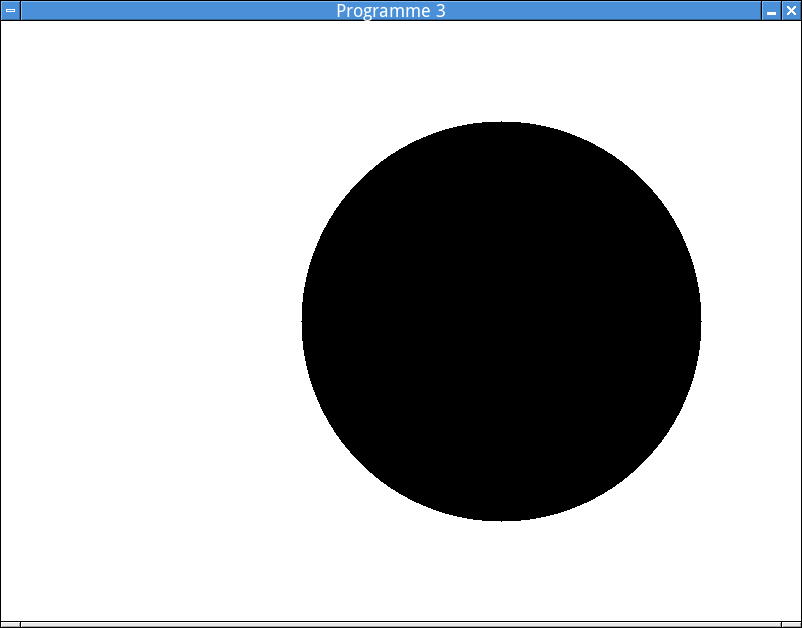
   • Pour afficher un nombre, on dessine un disque de la couleur appropriée et de 10 pixels de rayon, centré sur le point correspondant de la fenêtre.

3. Testez votre programme en affichant les nombres \(-1.5 - 0.5i\) et \(0.5 - i\) en rouge, et leur conjugué en bleu. Vous devriez obtenir une image similaire à celle-ci:

   

   Affichage du programme 1.

4. Déposez votre programme dans le répértoire centralisé des laboratoires:

   • Placez-vous dans le répertoire /home/boigelot/lab-mp-2/labo-1.
   • Recopiez-y votre programme dans un fichier appelé nom1-nom2-nom3--prog-1.py, où le préfixe contient les noms des membres de votre groupe. (Vous pouvez bien sûr l’adapter à la taille de votre groupe. En cas d’homonymie, veillez à indiquer également votre prénom.)
   • Protégez ce fichier contre la lecture grâce à la commande chmod 600 nom-du-fichier.

Les racines de l’unité

Le deuxième programme que vous allez rédiger vous fait manipuler des racines de l’unité. L’énoncé est simple:

• On considère le nombre complexe \(c = \cos\theta + i\sin\theta\), avec \(\theta = 2\pi\frac{p}{q}\), où \(p\) et \(q\) sont des nombres entiers (avec bien sûr \(q \neq 0\).)

• On étudie le comportement de la suite \(z_0\), \(z_1\), \(z_2\), \(z_3\), …, où

  \(z_0 = c\),

  et pour tout \(i \in \mathbb{N}\):

  \(z_{i+1} = c\, z_i\).

Procédure à suivre:

1. Ecrivez un programme qui affiche les termes \(z_i\) successifs de la suite, pour des valeurs de \(p\) et de \(q\) données, et pour un nombre d’itérations fixé (par exemple, 10000). Pour vous simplifier la vie, n’hésitez pas à partir du programme précédent, et à exploiter au maximum les fonctions de votre bibliothèque de manipulation de nombres complexes.
2. Expérimentez avec différentes valeurs de \(p\) et de \(q\). (Suggestions pour commencer: \((p, q) = (1, 7)\), \((p, q) = (5, 7)\), \((p, q) = (117, 480)\), \((p, q) = (320, 480)\)).
3. Seriez-vous capable de déterminer directement, pour \(p\) et \(q\) donnés, combien d’itérations sont nécessaires pour atteindre \(z_i = 1\), et de le justifier mathématiquement? Si oui, modifiez votre programme de façon à arrêter les itérations dès que cette valeur est atteinte.
4. Déposez votre programme dans le répértoire centralisé, sous le suffixe prog-2.py.

Génération de figures fractales

Les suites de nombres complexes peuvent avoir un comportement beaucoup plus intéressant que celle que vous venez d’étudier. Nous allons à présent examiner la suite

\(z_0 = 0\),

et pour tout \(i \in \mathbb{N}\):

\(z_{i+1} = z_i ^ 2 + c\),

en fonction de la valeur de \(c\). (Note: Le carré \(z^2\) d’un nombre complexe \(z\) est, sans surprise, égal au produit de ce nombre par lui-même.)

On souhaite déterminer, pour \(c\) donné, si les valeurs successives de cette suite restent dans une zone du plan complexe proche de 0, ou bien si elles en sortent.

La zone que nous allons considérer est celle qui contient tous les nombres dont le module est inférieur ou égal à 2. En d’autre termes, la question que nous nous posons pour une valeur de \(c\) donnée est la suivante:

Existe-t-il une valeur de \(i\) pour laquelle on a \(|z_i| > 2\) ?

Votre objectif consiste à rédiger un programme capable de déterminer, pour chaque point \(c\) du plan complexe, si la réponse à cette question est vraie ou fausse. Pour ce faire, ce programme va:

• balayer l’ensemble des pixels de la fenêtre, et
• pour chacun d’entre eux, calculer les valeurs de la suite jusqu’à un nombre d’itérations donné. Si la condition \(|z_i| > 2\) devient vraie avant d’avoir atteint ce nombre d’itérations, on colore le pixel correspondant en blanc. Sinon, on le colore en noir.

Pour implémenter cet algorithme, vous aurez besoin de deux nouveaux mécanismes:

• Si l’on souhaite que l’affichage soit efficace, il n’est pas raisonnable d’invoquer une fonction de Pygame pour modifier individuellement chaque pixel. Une meilleur approche consiste à créer un tableau de pixels correspondant au contenu de la fenêtre, dont on peut alors directement modifier les éléments. Cette opération peut s’effectuer en évaluant pygame.PixelArray(fenetre), où fenêtre correspond au résultat retourné par pygame.display.set_mode() lors de l’initialisation de la fenêtre. La valeur retournée par pygame.PixelArray(fenetre) est un tableau dans lequel il est directement possible de modifier la couleur d’un pixel.

• Pour rappel, les opérations graphiques sont effectuées par Pygame dans une mémoire de travail qui n’est pas directement visible à l’écran. Après avoir réalisé de telles opérations, il ne faut pas oublier de recopier le contenu de cette mémoire vers la fenêtre, en invoquant pygame.display.flip().

  Dans le cas présent, vous serez amenés à traiter un grand nombre de pixels, et pour chacun d’entre eux, à effectuer un nombre non négligeable d’opérations de calcul. Cette procédure prendra donc du temps, et ce n’est pas une bonne idée d’attendre qu’elle soit terminée pour en afficher les résultats. Une possibilité est d’invoquer pygame.display.flip() chaque fois que l’on a mis à jour un certain nombre de pixels, par exemple une colonne complète. L’inconvénient de cette solution est que cette fonction met à jour l’ensemble de la fenêtre, plutôt que la zone restreinte correspondant aux dernières modifications, ce qui est inefficace. Pour pallier cet inconvénient, on peut plutôt utiliser la fonction pygame.display.update(rect) qui ne met à jour que la zone correspondant au rectangle rect.

A titre d’exemple, le programme suivant colorie individuellement tous les pixels de la fenêtre:

import pygame
import sys

### Constante(s)

BLANC = (255, 255, 255)
NOIR = (0, 0, 0)

### Fonction(s)

def traiter_evenements():
    for evenement in pygame.event.get():
        if evenement.type == pygame.QUIT:
            pygame.quit()
            sys.exit();
    return

### Paramètre(s)

dimensions_fenetre = (800, 600)  # en pixels

### Programme

# Initialisation

pygame.init()

fenetre = pygame.display.set_mode(dimensions_fenetre, 0)
pygame.display.set_caption("Exemple de coloriage");

pixels = pygame.PixelArray(fenetre)

# Dessin

fenetre.fill(BLANC)
pygame.display.flip();

for i in range(dimensions_fenetre[0]):
    for j in range(dimensions_fenetre[1]):
        pixels[i][j] = NOIR

    pygame.display.update(((i, 0), (1, dimensions_fenetre[1])))
    traiter_evenements()

# Boucle principale

while True:
    traiter_evenements()
    pygame.time.wait(25)

Note: Après avoir affiché une nouvelle colonne, ce programme examine également les évènements provoqués par l’utilisateur afin de détecter rapidement si celui-ci souhaite fermer la fenêtre. Il est toujours pertinent de procéder ainsi dans le cas d’un programme effectuant de longs calculs, afin que l’interface utilisateur de ce programme reste toujours réactive.

Procédure à suivre:

1. En vous basant sur le programme ci-dessus, et en y incorporant votre bibliothèque de manipulation de nombres complexes, écrivez un programme qui balaie le plan complexe pixel par pixel depuis le coin inférieur gauche \(-2.5 - 1.5i\) vers le coin supérieur droit \(1.5 + 1.5i\).

2. Testez votre programme en affichant en noir les points \(c\) tels que \(|c| < 1\), et en blanc les autres points. Vous devriez obtenir l’image suivante:

   

   Affichage du programme de test.

3. Créez une fonction test_convergence() qui calcule les termes de la suite

   \(z_0 = 0\),

   \(\forall i \in \mathbb{N}:\, z_{i+1} = z_i ^ 2 + c\),

   pour un nombre \(c\) donné, avec un nombre maximal d’itérations fixé (par exemple, à 200). Si une valeur satisfaisant \(|z_i| > 2\) est atteinte au cours de ces itérations, la fonction doit retourner False. Sinon, elle doit retourner True.

4. Faites colorier par votre programme chaque point \(c\) du plan complexe affiché dans la fenêtre en noir si test_convergence(c) est vrai, et en blanc sinon. Vous devriez obtenir le résultat suivant:

   

   Affichage du programme 3.

5. Déposez votre programme dans le répértoire centralisé, sous le suffixe prog-3.py.

L’ensemble de Mandelbrot en couleurs

L’ensemble des points coloriés en noir par votre dernier programme est appelé ensemble de Mandelbrot. Il possède des propriétés fascinantes; en particulier, sa frontière présente une structure dite fractale: En agrandissant certaines zones de cette frontière, on y retrouve des structures similaires à l’ensemble global.

(Pour mettre en évidence cette propriété d”autosimilarité, vous pouvez par exemple modifier les paramètres de votre programme pour explorer la région du plan complexe située entre le point inférieur gauche \(-0.6015 + 0.66i\) et le point supérieur droit \(-0.5935 + 0.666i\).)

Afin de mieux visualiser la structure de l’ensemble de Mandelbrot, nous allons maintenant l’afficher en couleurs. L’idée est, pour les points \(c\) pour lesquels la suite \(z_{i+1} = z_i ^2 + c\) diverge, de compter le nombre d’itérations \(i\) nécessaires pour satisfaire \(|z_i| > 2\), et d’attribuer la couleur du pixel correspondant en fonction de la valeur de \(i\).

Procédure à suivre:

1. Créez une fonction couleur(n) chargée de retourner la couleur associée au nombre d’itérations n, selon les principes suivants:

   • Une couleur est un tuple (rouge, vert, bleu) dont les composantes fondamentales possèdent une valeur comprise entre 0 (cette composante est absente) à 255 (cette composante est présente à 100%).
   • Le cas où n est égal à 0 correspond au cas particulier où l’on a une convergence, et doit produire la couleur noire .
   • Pour les autres valeurs de n, on procède comme suit:
     • Les valeurs entre 1 et 25 produisent une rampe linéaire entre les couleurs (0, 255, 255) (turquoise) et (255, 0, 255) (mauve).
     • Les valeurs entre 26 et 50 produisent une rampe linéaire entre les couleurs (255, 0, 255) (mauve) et (255, 255, 0) (jaune).
     • Les valeurs entre 51 et 75 produisent une rampe linéaire entre les couleurs (255, 255, 0) (jaune) et (0, 255, 255) (turquoise).
     • Ce cycle se répète de la même façon pour les valeurs supérieures à 75.

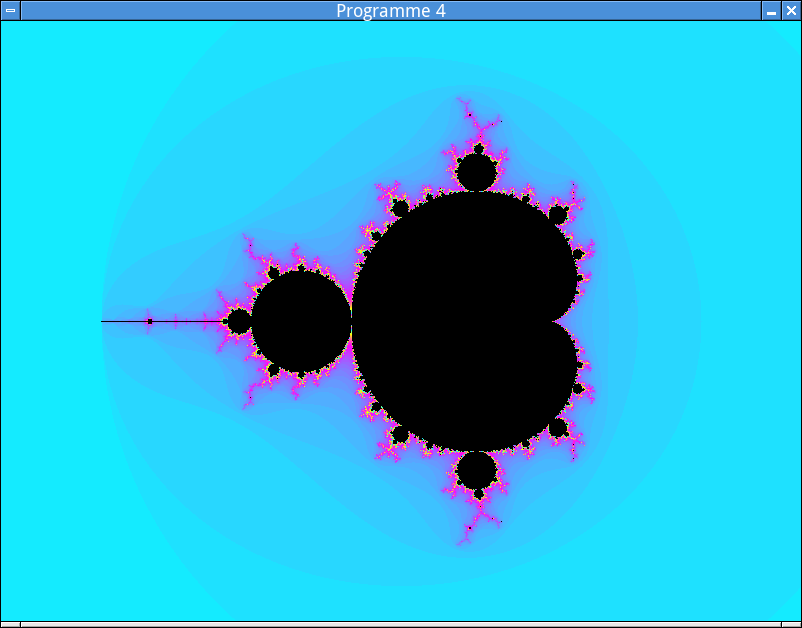
2. Modifiez la fonction test_convergence() de votre programme de façon à ce qu’elle retourne la couleur qui doit être associée à un pixel, en exploitant la fonction couleur() obtenue au point précédent.

3. Modifiez le fragment de code invoquant cette fonction de façon à colorier les pixels balayés par votre programme. Celui-ci devrait à présent produire un résultat similaire à celui-ci:

   

   Affichage du programme 4.

4. Déposez votre programme dans le répértoire centralisé, sous le suffixe prog-4.py.

Avec cette nouvelle version du programme, vous pouvez à nouveau explorer des zones intéressantes du plan complexe, comme par exemple les rectangles situés entres les points

• \(-0.6015 + 0.66i\) et \(-0.5935 + 0.666i\) (avec max. 400 itérations/pixel).
• \(0.295 + 0.4835i\) et \(0.2958 + 0.4841i\) (avec max. 1000 itérations/pixel).

Les ensembles de Julia

Le dernier projet de ce laboratoire consiste à générer des ensembles de Julia, qui sont égalements liés au comportement de la suite \(z_{i+1} = z_i ^2 + c\). L’idée consiste toujours à déterminer si cette suite diverge ou non après un nombre d’itérations fixé, mais à la différence de l’ensemble de Mandelbrot:

• On fixe maintenant la valeur de \(c\), qui reste identique pour tous les pixels de l’image.
• On détermine si la suite diverge ou non en explorant les valeurs du terme initial \(z_0\).

Cette procédure produit des images intéressantes pour des valeurs de \(c\) situées à proximité de la frontière de l’ensemble de Mandelbrot. Vous allez dès lors construire un programme qui gère une fenêtre avec deux parties:

• Dans la partie gauche, on dessine l’ensemble de Mandelbrot comme dans le programme 4.
• Lorsque l’utilisateur clique sur un point de l’image affichée dans cette partie gauche, on dessine dans la partie droite l’ensemble de Julia correspondant à la valeur de \(c\) ainsi désignée.

Procédure à suivre:

1. Modifiez votre dernier programme de façon à ce qu’il crée une fenêtre de 1600 x 600 pixels. Ce programme doit continuer à afficher l’ensemble de Mandelbrot dans la moitié gauche de cette fenêtre.

2. Modifiez la fonction traiter_evenements() de façon à lui faire également détecter les clics de la souris. Ceux-ci sont caractérisés par un champ type égal à pygame.MOUSEBUTTONDOWN, un champ button donnant le numéro du bouton sur lequel on a cliqué, et un champ pos retournant les coordonnées dans la fenêtre du point cliqué.

   L’objectif consiste à détecter les clics gauches de la souris dans la moitié gauche de la fenêtre, et de calculer les coordonnées correspondantes dans le plan complexe. Ensuite, le plus simple est de mettre à jour trois variables globales:

   • deux réels re_c et im_c donnant les valeurs réelle et imaginaire du point \(c\) désigné par l’utilisateur.
   • un booléen nouveau_clic que l’on rend vrai pour indiquer que l’utilisateur vient de cliquer sur un nouveau point.

   Note: N’oubliez pas de déclarer ces trois variables à l’aide du mot-clé global dans la fonction traiter_evenements().

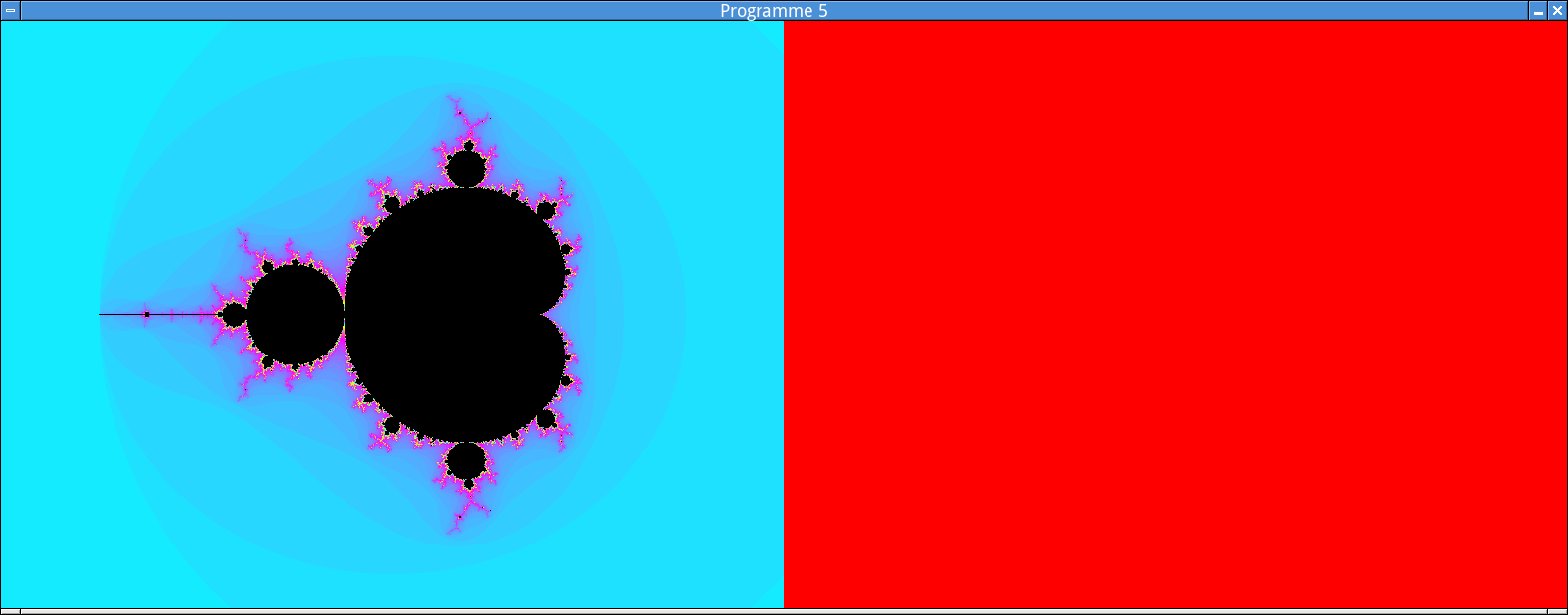
3. Dans la boucle principale du programme, après avoir terminé de dessiner l’ensemble Mandelbrot, il faut à présent détecter les situations où nouveau_clic est vraie. Lorsque cela se produit, cette variable doit revenir à la valeur fausse, et un balayage des pixels situés dans la moitié droite de la fenêtre doit être entamé.

   • Dans un premier temps, contentez-vous de peindre ces pixels dans une couleur constante (par exemple, en rouge), vous permettant de tester que cette partie du programme se comporte correctement.

   • N’oubliez pas d’invoquer traiter_evenements() et pygame.display_update() après avoir balayé chaque colonne, comme vous le faites lors de la génération de l’ensemble de Mandelbrot.

   • Lorsque traiter_evenements() détecte un nouveau clic (c’est-à-dire, lorsque nouveau_clic devient vraie), il faut interrompre le balayage qui est éventuellement en cours, et le recommencer depuis le début.

     Note: En Python, l’instruction break permet de sortir d’une boucle.

     A ce stade, votre programme devrait produire l’affichage suivant chaque fois que vous cliquez dans la moitié gauche de la fenêtre:

     

     Test du programme 5.

4. L’étape suivante consiste à effectuer, pour chaque pixel balayé, un test de convergence à l’aide de la même fonction test_convergence() que pour l’ensemble de Mandelbrot. La valeur de \(c\) est donnée par (re_c, im_c) (calculé par traiter_evenements()), et la valeur initiale \(z_0\) à considérer correspond aux coordonnées du pixel balayé dans le plan complexe.

   Pour l’ensemble de Julia, le mieux est d’utiliser \(-2 - 1.5i\) comme coin inférieur gauche de l’image, et \(2 + 1.5i\) comme coin supérieur droit. Dans votre boucle de balayage, effectuez la conversion entre les coordonnées des pixels balayés et le plan complexe en utilisant ces bornes.

   Il vous reste maintenant à modifier légèrement la fonction test_convergence() afin d’y ajouter deux paramètres supplémentaires:

   • Le premier correspond à la valeur de \(z_0\) à utiliser. N’oubliez pas d’attribuer la valeur 0 à ce paramètre dans le calcul de l’ensemble de Mandelbrot.
   • Le second permet, si vous ne l’avez pas déjà défini, de choisir le nombre maximal d’itérations à effectuer. Il est en effet utile de pouvoir choisir une valeur différente pour l’ensemble de Mandelbrot (typiquement, 200) et pour les ensembles de Julia (typiquement, 1000, ou même 5000 pour certaines valeurs intéressantes de \(c\)).

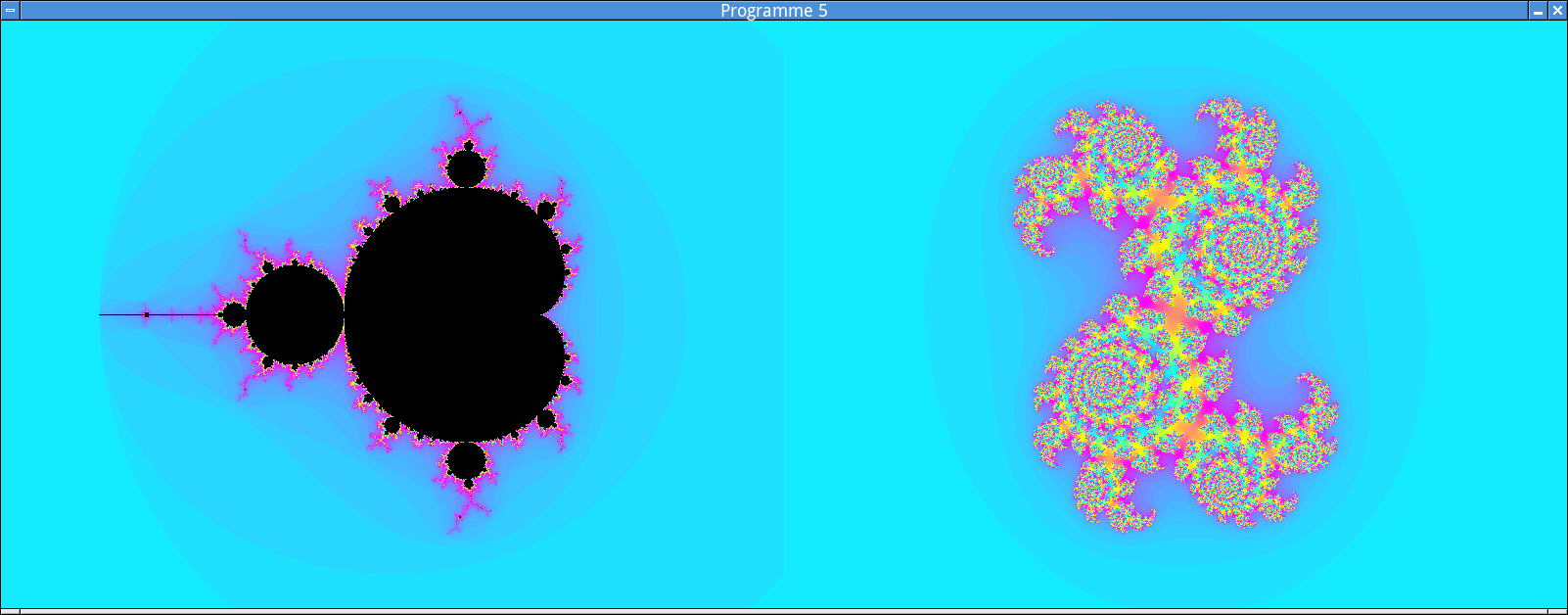
   La dernière étape consiste à attribuer à chaque pixel balayé la couleur retournée par test_convergence().

   Voici un exemple d’image genérée par le programme, après avoir cliqué près d’un point de la « vallée » située à la frontière droite de l’ensemble de Mandelbrot, près de l’axe réel.

   

   Exemple d’ensemble de Julia produit par le programme 5.

5. Déposez votre programme dans le répértoire centralisé, sous le suffixe prog-5.py.

Si vous êtes arrivé au terme cette étape avec un programme qui fonctionne, félicitations!

Il existe beaucoup de façons d’améliorer le programme que vous avez créé: En permettant à l’utilisateur de zoomer sur des régions particulières du plan complexe ou de sauvegarder les images obtenues, en optimisant les calculs en exploitant les symétries, en explorant d’autres fonctions que \(z^2 + c\) … Ne vous privez pas d’expérimenter!