
Le but de cette page n'est pas de proposer un cours de trigonométrie, avec études complètes, remarques, démonstrations et développements, mais bien de fournir un résumé le plus exhaustif possible.
Si vous découvrez des erreurs ou omissions, merci de me contacter. Cyril Briquet Table des matières : Formules fondamentales :
Relations trigonométriques de base
Analyse mathématique
Géométrie du triangle
Applications amusantes
[ Retour à la table des matières ]
Tableau des valeurs des fonctions trigonométriques prises en des points remarquables :

[ Retour à la table des matières ]
Décomposition des arguments composés :
 b) = sin a . cos b
b) = sin a . cos b  cos a . sin b
cos a . sin b
 b) = cos a . cos b
b) = cos a . cos b  sin a . sin b
sin a . sin b
 b) = (tg a
b) = (tg a  tg b) / (1
tg b) / (1  tg a . tb b)
tg a . tb b)
[ Retour à la table des matières ]
Angles associés :
Grands associés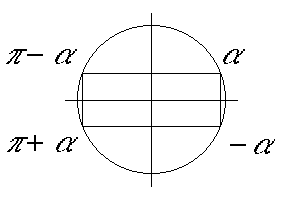
f_trigo[grand_associé_de_alpha] |
Petits associés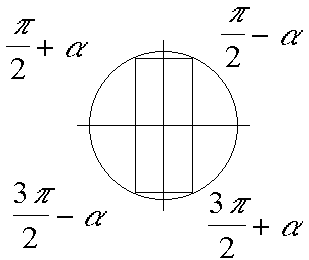
f_trigo[petit_associé_de_alpha] |
 + a] = - tg a
+ a] = - tg a
 / 2) - a] = - cos a
/ 2) - a] = - cos a
[ Retour à la table des matières ]
Développements selon les arguments doubles (cas de décomposition d'arguments composés quand a = b) :
[ Retour à la table des matières ]
Développements selon les arguments triples :
[ Retour à la table des matières ]
Formules de Carnot (formulation pratique du développement selon les arguments doubles) :
[ Retour à la table des matières ]
Formules de Simpson pour le produit
(diminution d'ordre 1 du degré polynomial) :
| cos a . cos b = | 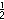 | [ cos(a-b) + cos(a+b) ] |
| sin a . sin b = | 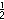 | [ cos(a-b) - cos(a+b) ] |
| sin a . cos b = | 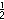 | [ sin(a-b) + sin(a+b) ] |
[ Retour à la table des matières ]
Formules de Simpson pour la somme
(augmentation d'ordre 1 du degré polynomial) :
| cos a + cos b = 2 cos | 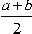 | . cos | 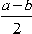 |
| cos a - cos b = -2 sin | 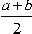 | . sin | 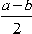 |
| sin a + sin b = 2 sin | 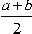 | . cos | 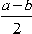 |
| sin a - sin b = 2 cos | 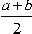 | . sin | 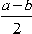 |
[ Retour à la table des matières ]
Développements tangentiels :
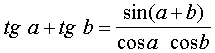
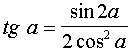 | (cas particulier de la formule précédente quand a = b) |
[ Retour à la table des matières ]
Changement de variables dans le cadre du calcul d'intégrales de fonctions trigonométriques rationnelles :
[ Retour à la table des matières ]
Développements selon tg x/2 :
[ Retour à la table des matières ]
Quelques intégrales trigonométriques particulièrement intéressantes :
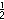 )=
)=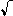
 ).
).
[ Retour à la table des matières ]
Tableau comparatif des fonctions trigonométriques circulaires et hyperboliques :
|
|
||||||
|---|---|---|---|---|---|---|---|
|
|
||||||
| cos² x + sin² x = 1 | ch² x - sh² x = 1 | ||||||
| 1 + tg² x = 1 / cos² x | 1 - th² x = 1 / ch² x | ||||||
| 1 + cotg² x = 1 / sin² x | 1 - coth²x = -1 / sh² x | ||||||
| exp(ix) = cos x + i sin x | exp(x) = ch x + sh x | ||||||
| exp(-ix) = cos x - i sin x | exp(-x) = ch x - sh x |
[ Retour à la table des matières ]
Forme logarithmique des fonctions hyperboliques réciproques [utile dans le cadre du calcul intégral] :
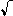 (x²+1)]
(x²+1)]
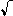 (x²-1)]
(x²-1)]
| arcth x = | 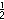 | ln [(1+x) / (1-x)] |
| arccoth x = | 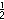 | ln [(x+1) / (x-1)] |
[ Retour à la table des matières ]
Etude sommaire des fonctions usuelles :
| f (x) | f ' (x) | Dom x | Dom y | Zéro |
|---|---|---|---|---|
| sin x | cos x | [ 0 ; +2 ] + 2k ] + 2k | [ -1 ; +1 ] | 0 + k |
| cos x | -sin x | [0 ; +2 ] + 2k ] + 2k | [ -1 ; +1] |  / 2 + k / 2 + k |
| tg x | 1 / cos² x | ] - / 2 ; + / 2 ; + / 2 [ + k / 2 [ + k | ] - ; + ; + [ [ | 0 + k |
| cotg x | -1 / sin² x | ] 0 ; + [ + k [ + k | ] - ; + ; + [ [ |  / 2 + k / 2 + k |
| arcsin x | 1 / 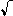 (1 - x²) (1 - x²) | [ -1 ; +1 ] | [ - / 2 ; + / 2 ; + / 2 ] / 2 ] | 0 |
| arccos x | -1 / 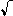 (1 - x²) (1 - x²) | [ -1 ; +1 ] | [ + ; 0 ] ; 0 ] | 1 |
| arctg x | 1 / (1 + x²) | ] - ; + ; + [ [ | ] - / 2 ; + / 2 ; + / 2 [ / 2 [ | 0 |
| arccotg x | -1 / (1 + x²) | ] - ; + ; + [ [ | ] + / 2 ; - / 2 ; - / 2 [ / 2 [ |  / 2 / 2 |
| sh x | ch x | ] - ; + ; + [ [ | ] - ; + ; + [ [ | 0 |
| ch x | sh x | ] - ; + ; + [ [ | [ +1 ; + [ [ | 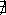 |
| th x | 1 / ch² x | ] - ; + ; + [ [ | ] -1 ; +1 [ | 0 |
| coth x | 1 / sh² x | ] - ; -1 [ U ] +1 ; + ; -1 [ U ] +1 ; + [ [ | ] - ; -1 [ U ] +1 ; + ; -1 [ U ] +1 ; + [ [ | 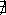 |
| arcsh x | 1 / 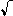 (x² + 1) (x² + 1) | ] - ; + ; + [ [ | ] - ; + ; + [ [ | 0 |
| arcch x | 1 / 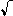 (x² - 1) (x² - 1) | [ +1 ; + [ [ | [ 0 ; + [ [ | 1 |
| arcth x | 1 / (1 - x²) [*1*] | ] -1 ; +1 [ | ] - ; + ; + [ [ | 0 |
| arccoth x | 1 / (1 - x²) [*2*] | ] - ; -1 [ U ] +1 ; + ; -1 [ U ] +1 ; + [ [ | ] - ; 0 [ U ] 0 ; + ; 0 [ U ] 0 ; + [ [ | 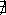 |
Remarques
 donnée (n naturel) à un scalaire, le résultat reste scalaire. Lorsque cette même quantité est ajoutée à un domaine de R², on considère qu'elle est en fait ajoutée à chacune des composantes, celles-ci restant individuellement scalaires de R, après addition.
donnée (n naturel) à un scalaire, le résultat reste scalaire. Lorsque cette même quantité est ajoutée à un domaine de R², on considère qu'elle est en fait ajoutée à chacune des composantes, celles-ci restant individuellement scalaires de R, après addition.
 ; -1 [ U ] +1 ; +
; -1 [ U ] +1 ; + [, complémentaire de l'ouvert ] -1 ; +1 [ sur R\{(-1,+1)}
[, complémentaire de l'ouvert ] -1 ; +1 [ sur R\{(-1,+1)}
[ Retour à la table des matières ]
Calcul des fonctions trigonométriques des demi-angles d'un triangle en fonction des cotés :
Remarques
[ Retour à la table des matières ]
Calcul des hauteurs d'un triangle
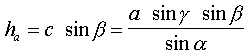
Remarques
[ Retour à la table des matières ]
Calcul des bissectrices d'un triangle
Remarques
[ Retour à la table des matières ]
Calcul des médianes d'un triangle
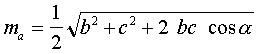
Remarques
[ Retour à la table des matières ]
Calcul du rayon du cercle inscrit d'un triangle
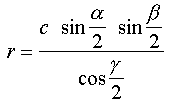
Remarque
[ Retour à la table des matières ]
Aire d'un triangle (diverses méthodes de calcul) :
Remarques
[ Retour à la table des matières ]
Dessiner des segments de droites de longueur irrationnelle algébrique à la règle et au compas :
Calcul (généralement on prend a et b appartenant à Q, l'ensemble des rationnels)Exemple
- longueur[diametre(cercle)] = a + b
- longueur[droite_a_dessiner] =
(a . b) = racine de (a . b)
- longueur[diametre(cercle)] = 3 + 4
- longueur[droite_a_dessiner] =
(3 . 4) = racine de 12
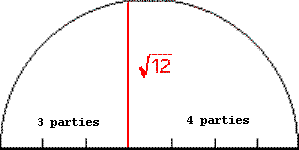
[ Retour à la table des matières ]
Un plus un = deux :
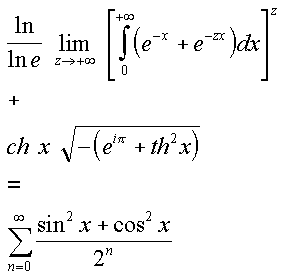
Très tôt, l'étudiant en Sciences Appliquées se rend compte qu'il n'est jamais de bon goût d'écrire l'égalité triviale 1 + 1 = 2 sous une forme aussi naïve (n'est-ce pas ?). Dès lors, grâce à une utilisation astucieuse des relations hyperboliques, de développements en série et de techniques avancées d'intégration réelle, nous pouvons nous émerveiller de l'embellissement suivant, que le lecteur averti appréciera pour sa clarté exemplaire. On exhibe ainsi qu'il est évident que le texte présenté est de loin plus clair et plus lisible sous sa nouvelle forme.
Remarque
[ Retour à la table des matières ]
Alphabet grec :

[ Retour à la table des matières ]