Discussion


Next: Conclusion
Up: Machine learningneural networks
Previous: Preventive security assessment
We have illustrated the application of various methods to emergency
and preventive voltage security assessment to derive criteria able to
anticipate a possible risk of voltage collapse in real-time and
trigger appropriate (emergency or preventive) control actions if
necessary.
In the emergency state detection problem, the investigation has been
based on usual operating parameters (e.g. power flows, voltages)
obtained from system snapshots made ``just after the occurrence of a
disturbance''. On the other hand, it is possible to use more
sophisticated ``features'' so as to improve accuracy; this was
illustrated in the preventive security example by the pre-disturbance
load power margin, which allowed to improve significantly the accuracy
of all the tested methods. We believe, however, that available
non-parametric computer based learning methods are sufficiently
powerful to exploit standard ``operating parameters''. A main
advantage is that this leads to a more systematic, and mostly
automatic approach, and that the resulting criteria are expressed in
terms of variables easily appraised by operators and engineers in
charge of security studies. Admittedly, to reach better accuracy,
larger learning sets may be needed; but these may be easily obtained
via random sampling and parallel simulations, where the price to pay
is mainly in terms of cheap computing power. This is also illustrated
by the larger training set size used in the preventive security
assessment example, which allows, despite the more stringent
conditions, to reach a very high level of accuracy.
The major tendencies which emerge from our comparative experiments are
the following.
The multi-layer perceptrons together with second order
optimization methods are a very flexible and easy to apply approach.
It provides generally very good results in terms of accuracy, although
at the expense of very slow learning, which may prevent easy
interactive experimentation; actually, for problem sizes of the order
of those encountered in large scale power system security applications
a reduction of at least two orders of magnitude in learning times
would be required. On the other hand, the MLPs are able to exploit
very effectively continuous security margins or indices, in particular
to improve accuracy. This is a main advantage shared with other
continuous regression methods like SMART, for example. However, at
the current stage of advancement the main drawback of these methods is
the ``black-box'' nature of the provided security criteria, which are
unable to tell their physical meaning. This is a significant
shortcoming, for without the ability to produce understandable
decisions, it is hard to be confident in the reliability of methods
that address real-world problems [30].
Decision trees appear to be by far the fastest method both at
the learning and at the prediction step. Together with their good
interpretability this efficiency enables us to ``play'' with them in
order to analyze a data base and acquire new physical insights. From
this respect they are rather unique. In particular, they are able to
explicitly identify among many candidate attributes those which
significantly influence the security status of the system. Further,
their step by step approach to decision making is quite close to the
reasoning of human experts; they are therefore easier to appraise,
criticize and accept by the latter. On the other hand, as concerns
accuracy many interesting sophistications have been proposed in the
literature, such as ``linear combination splits'' and ``regression
trees'' which are able to further improve them
[32][31]. However, the elementary trees we
used appear to be already of good accuracy while often easier to
interpret than more sophisticated ones.
The nearest neighbor method shows a rather erratic behavior in
terms of accuracy. Most often its performance in high dimensional
attribute spaces is very deceiving, but occasionally it may be very
good. This is because we use as attributes standard ``operating
parameters'' and because we have still no systematic methodology to
choose a proper distance or similarity measure in this attribute
space. Nevertheless, the results obtained so far are promising and we
believe that research should proceed in order to develop systematic
approaches to adapt distances to problem specifics. The nearest
neighbor method may be used in many ways, once an appropriate distance
has been found. For example, the distance of the nearest neighbor to
the current state may be used as a measure of the degree of confidence
one may attach to the diagnostic provided on the basis of the data
base. If the latter distance is too large, it would be concluded that
for the current state no reliable security information may be derived.
If, on the contrary, the nearest neighbors are sufficiently close to
the current state, various kinds of detailed and specific security
information may be extrapolated from these states to the current
situation, and shown to the operator. After all, the nearest neighbor
method replicates the way operators approach problems, by recalling
similar situations seen in the past.
Finally, the hybrid approaches show to be effective in
``rounding off'' corners of the ``box-type'' security regions defined
by decision trees. In particular the ``margin hybrid'' DT-ANN approach
is very promising in conciliating the simplicity of the trees and the
accuracy of multi-layer perceptrons.
As concerns accuracy, it is worth mentioning that for security
assessment problems it is in practice necessary to distinguish among
``false alarms'' and ``non-detections'' of insecurity. In the context
of our comparative study of learning methods we did not make this
distinction, which would render the interpretation of results more
complex, without affecting the main conclusions. Let us mention,
however, that there exist several alternative techniques which enable
us to reduce the risk of non-detections. For example, the most
straightforward approach may be used by any of the computer based
learning techniques; it consists merely of increasing slightly
the classification threshold of the load-power margin at the time of
learning the model, so as to introduce a sufficient bias in the
classification. On the other hand, in the context of regression
techniques (MLPs, SMART, 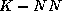 ...) allowing us to approximate security margins of unseen states,
we could as well increase the classification threshold at the time of
using the model. Both techniques show to be quite efficient in
practice, although the latter is more flexible than the former. Thus,
in the context of our preventive voltage security assessment example,
shifting the load-power margin threshold by about 35 MW enables us to
eliminate almost completely non-detections while increasing only
moderately the number of false alarms (
...) allowing us to approximate security margins of unseen states,
we could as well increase the classification threshold at the time of
using the model. Both techniques show to be quite efficient in
practice, although the latter is more flexible than the former. Thus,
in the context of our preventive voltage security assessment example,
shifting the load-power margin threshold by about 35 MW enables us to
eliminate almost completely non-detections while increasing only
moderately the number of false alarms (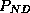 decreases from 2.25%
to 0.6 % while
decreases from 2.25%
to 0.6 % while 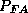 increases from 2.25% to 4.4%).
increases from 2.25% to 4.4%).


Next: Conclusion
Up: Machine learningneural networks
Previous: Preventive security assessment
Wed Jan 18 20:24:41 MET 1995
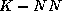 ...) allowing us to approximate security margins of unseen states,
we could as well increase the classification threshold at the time of
using the model. Both techniques show to be quite efficient in
practice, although the latter is more flexible than the former. Thus,
in the context of our preventive voltage security assessment example,
shifting the load-power margin threshold by about 35 MW enables us to
eliminate almost completely non-detections while increasing only
moderately the number of false alarms (
...) allowing us to approximate security margins of unseen states,
we could as well increase the classification threshold at the time of
using the model. Both techniques show to be quite efficient in
practice, although the latter is more flexible than the former. Thus,
in the context of our preventive voltage security assessment example,
shifting the load-power margin threshold by about 35 MW enables us to
eliminate almost completely non-detections while increasing only
moderately the number of false alarms (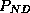 decreases from 2.25%
to 0.6 % while
decreases from 2.25%
to 0.6 % while 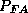 increases from 2.25% to 4.4%).
increases from 2.25% to 4.4%).