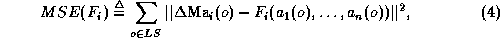Formulation of the regression problem


Next: Non-parametric regression techniques
Up: LOAD POWER MARGIN
Previous: Random generation of
In the above equation (1)  is the
contingency independent term while the two other terms are in practice
strongly contingency dependent, and it is clearly appropriate to build
the regression models in a single-contingency approach so as to
exploit the latter specificity.
is the
contingency independent term while the two other terms are in practice
strongly contingency dependent, and it is clearly appropriate to build
the regression models in a single-contingency approach so as to
exploit the latter specificity.
Thus, for a given contingency we select its learning set (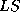 ) as the
relevant operating states (denoted
) as the
relevant operating states (denoted  below) for this contingency
among the
below) for this contingency
among the 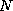 first of the data base. Each state is characterized
by : (i)
first of the data base. Each state is characterized
by : (i)  candidate attributes
candidate attributes 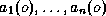 describing its topology (e.g. in/out indicators) and electrical state
(e.g. voltages, power flows, generation levels, reactive reserves
...) which are deemed to influence the severity of the contingency
and in terms of which it is desired to express the regression models;
(ii) its difference
describing its topology (e.g. in/out indicators) and electrical state
(e.g. voltages, power flows, generation levels, reactive reserves
...) which are deemed to influence the severity of the contingency
and in terms of which it is desired to express the regression models;
(ii) its difference 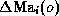 of its pre-computed values
of
of its pre-computed values
of 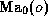 and
and 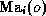 .
.
Then the learning objective is to build an approximate model,
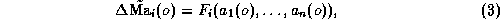
where the function 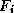 is determined so as to ``explain'' as much as
possible the variance of
is determined so as to ``explain'' as much as
possible the variance of 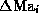 observed in the learning
set, e.g. such that the Mean Square Error (MSE)
observed in the learning
set, e.g. such that the Mean Square Error (MSE)
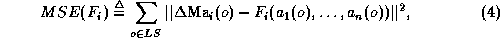
is as small as possible. Notice that this calls for the
identification among the candidate attributes of a subset of
attributes which are actually relevant, i.e. which actually influence
the severity of the particular contingency under consideration. We
conjecture that for each contingency it is possible to identify a
small number of attributes able to explain most of the variance of its
severity. Obviously, these salient attributes are liable to change
significantly from one contingency to another.
Wed Jan 18 20:00:51 MET 1995
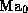 is the
contingency independent term while the two other terms are in practice
strongly contingency dependent, and it is clearly appropriate to build
the regression models in a single-contingency approach so as to
exploit the latter specificity.
is the
contingency independent term while the two other terms are in practice
strongly contingency dependent, and it is clearly appropriate to build
the regression models in a single-contingency approach so as to
exploit the latter specificity.
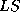 ) as the
relevant operating states (denoted
) as the
relevant operating states (denoted  below) for this contingency
among the
below) for this contingency
among the 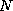 first of the data base. Each state is characterized
by : (i)
first of the data base. Each state is characterized
by : (i)  candidate attributes
candidate attributes 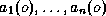 describing its topology (e.g. in/out indicators) and electrical state
(e.g. voltages, power flows, generation levels, reactive reserves
...) which are deemed to influence the severity of the contingency
and in terms of which it is desired to express the regression models;
(ii) its difference
describing its topology (e.g. in/out indicators) and electrical state
(e.g. voltages, power flows, generation levels, reactive reserves
...) which are deemed to influence the severity of the contingency
and in terms of which it is desired to express the regression models;
(ii) its difference 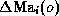 of its pre-computed values
of
of its pre-computed values
of 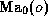 and
and 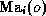 .
.
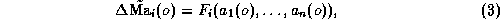
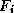 is determined so as to ``explain'' as much as
possible the variance of
is determined so as to ``explain'' as much as
possible the variance of 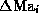 observed in the learning
set, e.g. such that the Mean Square Error (MSE)
observed in the learning
set, e.g. such that the Mean Square Error (MSE)