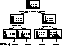
Figure 4: Regression tree for line tripping contingency
Similarly to decision (or classification) trees, regression trees decompose the attribute space into a hierarchy of regions. In our application they will decompose the pre-disturbance operating space of a power system into regions where the severity of a contingency is as constant as possible. In each such region the severity will be estimated by its expected value determined in the corresponding learning sub-sample.

Figure 4: Regression tree for line tripping contingency
Similarly to decision trees, regression trees are built in a top-down
approach : starting with the top-node (e.g. see Fig.
4) and the complete learning set, an
attribute 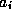 and a threshold value
and a threshold value 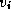 are selected to decompose
the learning set into two subsets, corresponding to states for which
are selected to decompose
the learning set into two subsets, corresponding to states for which
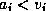 and
and 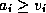 respectively. The split is determined
so as to reduce as much as possible the severity variance in the
subsets, or in other words to provide a maximum amount of information
on the severity.
respectively. The split is determined
so as to reduce as much as possible the severity variance in the
subsets, or in other words to provide a maximum amount of information
on the severity.
The procedure continues splitting until either the variance has been sufficiently reduced or it is not possible to reduce it further in a statistically significant way. The latter may happen due to either a reduced subsample size or a low predictive value of the candidate attributes at a tree node.
In our simulations we have used the method described in [8] together with its post-pruning algorithm to avoid overfitting.
For prediction, the regression tree is used similarly to a decision tree : a new state is directed through the tree, by starting at the top-node and applying the encountered tests to direct the state towards the appropriate successor. When a terminal node is reached, the there stored mean value (or confidence interval) is used as an estimate of the severity. It thus provides a piecewise constant model which is particularly well adapted to represent the effect of topology as well as electrical state. On the other hand, due to its interpretability and capability to identify the attributes which influence most strongly the severity, it is an appropriate data analysis tool for validation.
The main practical difference between decision and regression trees is that the latter determine automatically the appropriate quantization of the severity into subintervals, whereas the former merely reproduce a predefined classification.