The corresponding data base was passed to the researchers of the StatLog project, who used it to compare a wide range of methods; Table 1 collects results obtained. Before commenting on them we briefly describe the used classification methods; for further information, we refer the interested reader to [3].
Table: Academic system results obtained in the StatLog project. Adapted from
[3]
Among the statistical methods the first three are parametric ones using linear and quadratic models. The other four are non-parametric ones. SMART denotes the projection pursuit method [29], Kernel density denotes the Parzen estimator and the Naive Bayesian approach consists of assuming class-conditional independence of attribute values and using one-dimensional histograms to estimate attribute probability densities in each class.
Most of the machine learning methods are TDIDT algorithms (Cart, Indcart, NewID, AC2, BayTree, C4.5, Cal5) while ITrule and CN2 are rule learning algorithms and Castle builds causal polytrees.
Among the neural network based algorithms we note that Dipol92, MLP and Radial Basis Functions are three different supervised feed-forward architectures, while the two others correspond to unsupervised (SOM) and supervised (LVQ) versions of Kohonen's self-organizing map.
We observe that SMART together with the logistic discriminant produce
significantly better results than the other algorithms (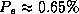
); but SMART is about 50 times slower than the logistic
discriminant. The neural network algorithms (MLP and Dipol92) provide
also very good results (
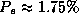). The TDIDT algorithms
provide intermediate results (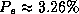
), similar to those
obtained below. On the other hand, the Kohonen SOM (and LVQ) as well
as the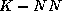 
method are much less accurate (
).
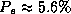A possible explanation of the good performance of the linear model (Logist. Discrim.) is the reduced problem size of the present example, which certainly plays in favor of the parametric estimation techniques. Thus, this is not likely to hold in general.
We note the high sensitivity of the linear models (Lin. Discrim vs Logist. Discrim.) to the learning criterion used. On the other hand, the results obtained with the various TDIDT approaches are quite close to each other, which suggests that these non-parametric approaches are quite robust with respect to changes in their learning criterion.
We obtained additional results with decision trees, direct (i.e.
non-hybrid) and hybrid MLPs, and direct and hybrid 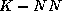classifiers.
A decision tree, built on the basis of the 28 candidate attributes is
shown in Fig. 4. It is composed of 7 test nodes and 8
terminal nodes. Its top node corresponds to the complete learning
set, composed of 454 critical and 796 non-critical states
. Out of the 28 candidate attributes only three have actually
been selected to formulate the tree. In fact, two of these, V4 and
Res7, are found to carry 97% of the information of the decision tree.
When used to classify the 1250 unseen test states, the decision tree
realizes 96.24% correct recognitions. Thus, despite its simplicity,
it is able to correctly represent voltage security behavior of the
considered system. Among the 47 classification errors of the tree
there were 15 non-detections (i.e.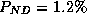 
of critical states
classified non-critical by the tree) and 32 false alarms (i.e. 
of non-critical states classified critical by the tree).
Figure: Academic system tree. Adapted from [25]
Table 2 summarizes our results. The direct MLP's input layer corresponds to the 28 candidate attributes, and we have used only a single hidden layer corresponding to 25 neurons. The two neurons of the output layer correspond to the critical and non-critical classes; a state is classified into the class corresponding to highest output neuron activation. The hybrid MLP uses only the 3 attributes selected by the decision tree as input variables; its two hidden layers correspond to the test and terminal nodes of the tree [23].
Similarly, the nearest neighbor classifier was applied either by using
the 28 candidate attributes in the distance computation or only the 3
test attributes of the DT. A range of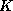 
values was screened; Table
2 lists the error rates corresponding to 
and
(which is the value yielding a minimal test set error rate).
Table: Academic system results obtained in Liège
All in all our results of Table 2 are consistent with
those of Table 1. We observe that the two hybrid
approaches are able to improve the classification of the decision
trees, while using only the three attributes selected by them : the
difference of about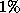 
between the error rate of the hybrid
approaches and the DT appears to be the price to pay for the
simplicity of the box type approximation to security regions provided
by the tree. On the other hand, a further reduction of 2% of the
error rate may be obtained by using the direct MLP approach : the
price to pay for this additional reduction in error rate appears to be
the use of 28 attributes instead of only three.
Finally it is interesting to notice that, in contrast to MLP, SMART or
Logistic discriminants, the 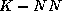method does not exploit properly
the 28 candidate attributes. This is a well known weakness of this
method which may have difficulties when the attribute space is of high
dimensionality. Therefore, it would not be useful as a stand-alone
method for realistic large scale security problems with large numbers
of candidate attributes.