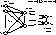
Figure 3: Feed forward multi-layer perceptron
The field of artificial neural networks has grown since the early work on perceptrons to an important and productive research field. We restrict ourselves to multi-layer perceptrons; for further information, a widely recommended theoretical introduction to neural networks is given in [12] while [13] gives a more exhaustive description of implementations and algorithms.
The single-layer perceptron, is basically a simple linear threshold unit together with an error correcting learning algorithm. It is able to represent a linear boundary in its input space. Its limited representation capabilities have motivated the consideration of more complex models composed of multiple interconnected layers of perceptrons, MLPs for short. Figure 3 illustrates the classical feed-forward MLP. The first or input layer corresponds to the attribute values, and the last or output layer to the desired classification or regression information. Intermediate layers enable the network to approximate arbitrary ``reasonable'' input/output mappings, provided that its topology and its weights are chosen appropriately.
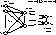
Figure 3: Feed forward multi-layer perceptron
The discovery of the back-propagation algorithm has been central to the success of MLPs [15][14]. It allows one to compute efficiently and locally the gradient of the output error of the network with respect to its weights and thresholds. It may be exploited iteratively in order to adjust the weights so as to reduce the total mean square output error for learning examples. In recent years, much progress has been made in using efficient optimization techniques for the learning procedures of MLPs; in our simulations we have used the so-called Broyden-Fletcher-Goldfarb-Shanno quasi-Newton method [16]. Despite these improvements, the MLPs are still very slow at the learning stage, which may prevent extensive experimentations for data base sizes typical of security assessment of realistic power systems.
Similarly to decision trees, an interesting property of MLPs is their ability to achieve feature extraction and learning in a single step : the weights connecting the input layer with the first hidden layer may be interpreted as projecting the input vector in some particular directions, realising a linear transformation of the input space, which is used in subsequent layers to approximate outputs. However, one of the difficulties with MLPs comes from the very high number of weights and thresholds related in a non-linear fashion, which makes it almost impossible to give any insight on the relationship learned. All in all, one can say that MLPs offer a flexible, easy to apply, but essentially black-box type of approach to function approximation.
In the recent years various neural network techniques have been applied to static as well as dynamic security assessment problems [20][19][18][17].