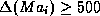LINE TRIPPING AND CORRESPONDING REGRESSION TREE

Unfortunately, all contingencies are not so simple. For example, considering the scatter plot corresponding to the line tripping contingency (loss of Circuit 1 of the double circuit line shown in Fig. 5), we observe that its variability is much higher although its mean severity (97MW) is similar to that of the preceding contingency. In particular, the operating states shown on the lower part of the scatter plot of Fig. 6b correspond to very large severities (e.g. 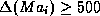MW). Thus, in the present case a less trivial model is required to predict the severity.

To illustrate the regression trees, we will describe in detail their application. However, for the sake of simplicity, and noting that the lost line is an important one allowing to import power to the load region from Plant 2, we will use only two candidate attributes : the total reactive reserve in Plant 2 and the logical status (in or out) of Circuit 2.

We consider the 4610 relevant states (i.e. where Circuit 1 is in operation) and put aside 1835 test states to assess the reliability of the tree. The remaining 2775 states are used as a learning set to build a regression tree, yielding the 3-level tree represented in Fig. 4. Each node of the tree is represented by a box containing a graphical representation of the distribution of values of 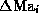in the learning set at this node, together with its sample mean value and standard deviation, and the number of its learning states (e.g. 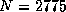at the top-node).

The tree is built in a top-down fashion, starting at the top-node, where the reactive reserve in Plant 2 is automatically selected as the best test attribute, together with its threshold value of 191Mvar. This test is determined by the tree building method so as to provide a maximum amount of information of the contingency severity in the learning set. Once the test has been selected, the learning set is split into two subsets, corresponding respectively to 1219 and 1556 states. This reduces the variance from 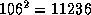at the top-node to a mean value of 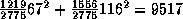at its successors.

Proceeding at both successors, we see that the selected test consists of checking whether Circuit 2 is in operation or not, which allows us to further reduce significantly the overall variance to a mean value of 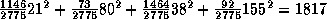. Thus, the regression tree explains 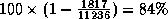of the variance of the severity.

Once the tree has been constructed, it may be used to estimate the contingency severity of an unknown state : to this end, we direct the state from the top-node to the appropriate successor according to its reactive reserve and further to a terminal node according to the status of Circuit 2. There, the severity is estimated by the mean severity of the corresponding learning states.

Let us discuss the physical interpretation of the tree.

L1.

The left most terminal node corresponds to 1146 pre-contingency states whose reactive reserve is smaller than 191Mvar while both circuits are in operation. The tree tells us that under these conditions the loss of one circuit is not severe at all, yielding a mean severity of 37MW with a standard deviation of 21MW, i.e. of the same order than the margin computation error.

L4.

Conversely, the right most terminal node tells us that if the reserve is rather high and already one circuit is out of operation, then the loss of the other circuit is a very severe contingency, leading to an expected reduction in load power margin of 547MW.

L3.

The slightly higher mean value and standard deviation of the severity at this node as compared to node L1, translates the fact that higher reactive reserves lead also to higher severities of the loss of a single circuit out of two.

L2.

This node is similar to L4, in that the only circuit in operation is lost; it tells us however that in this case the severity is not so important since not so much reactive reserve is available in Plant 2.

 
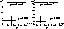
Figure 7: Computed vs estimated post-contingency LPMs 

Of course, the same error distribution is also obtained if we subtract the estimated severity from the pre-contingency LPM so as to estimate the post-contingency LPM, according to eqn. (1). This is illustrated in Fig. 7a showing the scatter plot of the test states in terms of their ``actual'' post-contingency load power margin and the estimated value of the latter. We notice that the estimated and actual LPMs are highly correlated. The correlation coefficient of 0.9923 indicates that overall the estimate is able to ``explain'' 98.5% of the variance of the post-contingency margin. This suggests that a very simple model may indeed provide valuable information about complex quantities such as post-contingency margins. To further fix ideas, we indicate that when using the estimated margin to classify the test states with respect to a threshold of 300MW (considering as unsecure the states for which the post-contingency margin is smaller than this threshold) leads to a classification error rate of 2.56%.

Giving a closer look at Fig. 7a, we observe that where the ``actual'' margin values are zero (i.e. if the contingency leads to a mid-term voltage instability without load increase), the estimated margin values become negative. Such negative margin values could for example be interpreted as the amount of emergency load shedding required to prevent a voltage instability.

To illustrate the possibility of exploiting the regression models to asses the impact of multiple contingencies, we use the tree to estimate the severity of the loss of two circuits.

We start with the hypothesis that the circuits are both in operation, and apply the tree to determine the severity of the first outage. If a new mid-term steady state is reached before the second circuit is lost, yielding in particular a change in the reactive reserve in Plant 2, we may apply the regression tree a second time in order to evaluate the impact of the loss of the second circuit. Notice that if the reactive reserve was initially smaller than 191Mvar, we might assume that it will remain smaller than this threshold after the loss of a circuit. Thus, in this particular case it is not necessary to recompute the steady state reached after the first outage to predict the effect of the second one; the severity of the double circuit outage is then estimated to 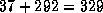MW. Remarkably, this is actually very close to the true mean severity (327MW) of the double circuit outage, as obtained in the same conditions by direct margin computation.