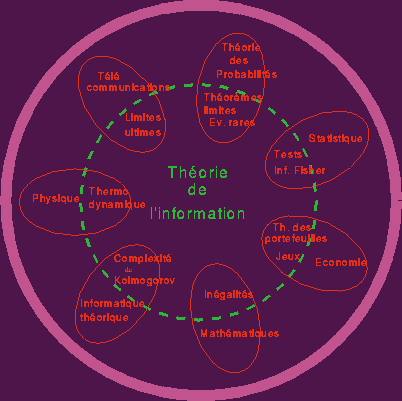
Information and coding theory
Louis Wehenkel
Université de Liège, Institut Montefiore
ELEN060-2
Lectures and Q&A sessions on Thursday PM:
1h30PM, Room R7, B28

|
Information and coding theoryLouis Wehenkel Université de Liège, Institut Montefiore ELEN060-2 Lectures and Q&A sessions on Thursday PM: 1h30PM, Room R7, B28 |